Cho biết cạnh mỗi ô vuông bằng \(1cm\). Tính độ dài các đoạn \(PQ,PR,RQ,AB,BC,CA\) trong Hình 11.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


hình tam giác đều thì độ dài các cạnh bằng nhau mà...

Áp dụng định lý Pitago trong tam giác vuông ABC ta có: (vì AB = AC) Từ đây suy ra . Lại có M là trung điểm của AC nên . |
Gọi I là trung điểm của BC, G là giao điểm của AI và BM, suy ra G là trọng tâm tam giác ABC, suy ra BM = 3GM (1). Do ABC là tam giác vuông nên AI = IB = IC, do đó tam giác IAC là tam giác cân tại I, suy ra (2) Lại có AM = MC (3). (4) Từ (2), (3) và (4) suy ra (c.g.c) Suy ra GM = NM (5). Từ (1) và (5) suy ra BM = 3NM (đpcm). |

Bài 1:
Áp dụng HTL trong tam giác vuông:
$AB^2=BH.BC$
$\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{10}=3,6$ (cm)
$CH=BC-BH=10-3,6=6,4$ (cm)
Tiếp tục áp dụng HTL:
$AH^2=BH.CH=3,6.6,4$
$\Rightarrow AH=4,8$ (cm)
$AC^2=CH.BC=6,4.10=64$
$\Rightarrow AC=8$ (cm)
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+1^2}=2$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{\sqrt{3}.1}{2}=\frac{\sqrt{3}}{2}$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{3-\frac{3}{4}}=\frac{3}{2}$ (cm)
$CH=BC-BH=2-\frac{3}{2}=\frac{1}{2}$ (cm)

Xin lỗi bn mink mới học có lớp 5 thôi à nên MINK ko thể giúp bn, xin lỗi nha

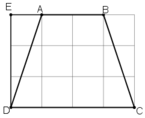
(Mỗi ô vuông là 1cm).
Nhìn vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD :
Xét tam giác vuông ADE có AE = 1cm, DE = 3cm.
⇒ AD2 = AE2 + DE2 (Định lý Pytago)
= 12 + 32 = 10
⇒ AD = √10 cm
+ Tính BC :
ABCD là hình thang cân nên BC = AD = √10 cm.
Vậy AB = 2cm, CD = 4cm, AD = BC = √10 cm.

TL
Chu vi hình tứ giác ABCD là:
1+1+1+1=4(cm)
ĐÁP SỐ 4 cm
HT
Đoạn thẳng \(AB\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{B^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AB = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(AC\) là đường chéo của hình chữ nhật với chiều dài là \(4cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(A{C^2} = {2^2} + {4^2} = 4 + 16 = 20 \Rightarrow AC = \sqrt {20} = 2\sqrt 5 \)
Đoạn thẳng \(BC\) là đường chéo của hình chữ nhật với chiều dài là \(6cm;\) chiều rộng là \(2cm\). Áp dụng định lí Py – ta – go ta được: \(B{C^2} = {2^2} + {6^2} = 4 + 36 = 40 \Rightarrow BC = \sqrt {40} = 2\sqrt {10} \)
Từ hình vẽ ta thấy:
\(Q\) là trung điểm của \(AC\);
\(R\) là trung điểm của \(AB\);
\(P\) là trung điểm của \(BC\).
- Vì \(Q\) là trung điểm của \(AC\); \(R\) là trung điểm của \(AB\) nên \(QR\) là đường trung bình của tam giác \(ABC \Rightarrow QR = \frac{1}{2}BC\) (tính chất đường trung bình)
\( \Leftrightarrow QR = \frac{1}{2}.2\sqrt {10} = \sqrt {10} \left( {cm} \right)\).
- Vì \(Q\) là trung điểm của \(AC\); \(P\) là trung điểm của \(BC\) nên \(QP\) là đường trung bình của tam giác \(ABC \Rightarrow QP = \frac{1}{2}AB\) (tính chất đường trung bình)
\( \Leftrightarrow QP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
- \(R\) là trung điểm của \(AB\); \(P\) là trung điểm của \(BC\) nên \(RP\) là đường trung bình của tam giác \(ABC \Rightarrow RP = \frac{1}{2}AC\) (tính chất đường trung bình)
\( \Leftrightarrow RP = \frac{1}{2}.2\sqrt 5 = \sqrt 5 \left( {cm} \right)\).
\(AB=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right);AC=\sqrt{4^2+2^2}=2\sqrt{5}\left(cm\right)\)
BC=căn 2^2+6^2=2*căn 10(cm)
Xét ΔABC có P,Q lần lượt là trung điểm của CB,CA
=>PQ là đường trung bình
=>\(PQ=\dfrac{AB}{2}=\sqrt{5}\left(cm\right)\)
Xét ΔABCcóQ,R lần lượt là trung điểm của AC,AB
=>QR là đường trung bình
=>\(QR=\dfrac{BC}{2}=\sqrt{10}\left(cm\right)\)
Xét ΔABC có P,R lần lượt là trung điểm của BC,BA
=>PR là đường trung bình
=>\(PR=\dfrac{AC}{2}=\sqrt{5}\left(cm\right)\)