\(\sqrt{x^2-10x+25}=2-x\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: TH1: x>=2
A=x+x-2=2x-2
TH2: x<2
A=x+2-x=2
b: TH1: x>=3
A=x-3-x=-3
TH2: x<3
A=3-x-x=-2x+3
c: TH1: x>=1
C=x-x+1=1
TH2: x<1
C=x+x-1=2x-1
d: TH1: m>=3
C=m-3-2m=-3-m
TH2: m<3
C=-m+3-2m=-3m+3
e: TH1: m>=1
E=m-m+1=1
TH2: m<1
E=m+m-1=2m-1

a) Ta có: \(\sqrt{x-2\sqrt{x-1}}-\sqrt{x-1}=1\)
\(\Leftrightarrow\left|\sqrt{x-1}-1\right|=\sqrt{x-1}+1\)
\(\Leftrightarrow\sqrt{x-1}=\sqrt{x-1}+1+1\)(Vô lý)
Vậy: \(S=\varnothing\)
b) Ta có: \(\sqrt{x^4+2x^2+1}=\sqrt{x^2+10x+25}-10x+22\)
\(\Leftrightarrow x^2+1=\left|x+5\right|-10x+22\)
\(\Leftrightarrow\left|x+5\right|=x^2+1+10x-22=x^2+10x-21\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=x^2+10x-21\left(x\ge-5\right)\\-x-5=x^2+10x-21\left(x< -5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+10x-21-x-5=0\\x^2+10x-21+x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2+9x-26=0\\x^2+11x-16=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-9+\sqrt{185}}{2}\\x=\dfrac{-11-\sqrt{185}}{2}\end{matrix}\right.\)

1) ĐKXĐ: \(x\ge\dfrac{5}{2}\)
\(\sqrt{x^2}=2x-5\\ \Rightarrow\left|x\right|=2x-5\\ \Rightarrow\left[{}\begin{matrix}x=2x-5\\x=5-2x\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=\dfrac{5}{3}\left(ktm\right)\end{matrix}\right.\)
2) ĐKXĐ: \(x\ge3\)
\(\sqrt{25x^2-10x+1}=2x-6\\ \Rightarrow\left|5x-1\right|=2x-6\\ \Rightarrow\left[{}\begin{matrix}5x-1=2x-6\\5x-1=6-2x\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{3}\left(ktm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge\dfrac{5}{2}\)
\(\sqrt{25-10x+x^2}=2x-5\\ \Rightarrow\left|x-5\right|=2x-5\\ \Rightarrow\left[{}\begin{matrix}x-5=2x-5\\x-5=5-2x\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=\dfrac{10}{3}\left(tm\right)\end{matrix}\right.\)
4) ĐKXĐ: \(x\ge\dfrac{1}{2}\)
\(\sqrt{1-2x+x^2}=2x-1\\ \Rightarrow\left|x-1\right|=2x-1\\ \Rightarrow\left[{}\begin{matrix}x-1=2x-1\\x-1=1-2x\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=\dfrac{2}{3}\left(tm\right)\end{matrix}\right.\)

\(a,\sqrt{x^2-10x+25}=x-2\\ ĐK:x-2\ge0\Leftrightarrow x\ge2\\ \sqrt{x^2-10x+25}=x-2\\ \Leftrightarrow x^2-10x+25=x^2-4x+4\\ \Leftrightarrow x^2-x^2-10x+4x=4-25\\ \Leftrightarrow-6x=-21\\ \Leftrightarrow x=\dfrac{7}{2}\left(tm\right)\\ Vậy.S=\left\{\dfrac{7}{2}\right\}\\ b,\sqrt{x+2}+\sqrt{9x+8}+\sqrt{4x+8}=2\\ \Leftrightarrow\sqrt{x+2}+3\sqrt{x+2}+2\sqrt{x+2}=2\\ \Leftrightarrow6\sqrt{x+2}=2\\ \Leftrightarrow\left[{}\begin{matrix}x+2\ge0\\\sqrt{x+2}=\dfrac{1}{3}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\ge-2\\x+2=\dfrac{1}{9}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\ge-2\\x=\dfrac{1}{9}-2\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\ge-2\\x=-\dfrac{17}{9}\left(tm\right)\end{matrix}\right.\\ Vậy.S=\left\{-\dfrac{17}{9}\right\}\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left|x+5\right|=x+5\\\left|x-5\right|=5-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5>=0\\x-5< =0\end{matrix}\right.\Leftrightarrow-5< =x< =5\)

a, \(\sqrt{4x^2+20x+25}\) + \(\sqrt{x^2-8x+16}\) = \(\sqrt{x^2+18x+81}\)
⇔ 4x2 + 20x + 25 + \(2\sqrt{\left(4x^2+20x+25\right)\left(x^2-8x+16\right)}\) = x2 + 18x + 81
⇔ 4x2 + 20x + 25 - x2 - 18x - 81 + \(2\sqrt{\left(2x+5\right)^2.\left(x-4\right)^2}\) = 0
⇔ 3x2 + 2x - 56 + 2.(2x + 5) . (x - 4) = 0
⇔ 3x2 + 2x - 56 + (4x + 10) . (x - 4) = 0
⇔ 3x2 + 2x - 56 + 4x2 - 16x + 10x - 40 = 0
⇔ 7x2 - 4x - 96 = 0
x1 = 4 ( nhận )
x2 = \(\frac{-24}{7}\) ( nhận )
Vậy: S = {4; \(\frac{-24}{7}\)}

\(\sqrt{x^2-25}+\sqrt{x^2+10x+25}=0.\)
\(\Rightarrow\sqrt{x^2-5^2}+\sqrt{x^2+2.5.x+5^2}=0\)
\(\Rightarrow\sqrt{\left(x-5\right).\left(x+5\right)}+\sqrt{\left(x+5\right)^2}=0\)
\(\Rightarrow\sqrt{\left(x+5\right).\left(x-5+1\right)}=0\)
\(\Rightarrow\hept{\begin{cases}x+5=0\\x-5+1=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-5\\x-4=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-5\\x=4\end{cases}}\)
Vậy \(x=\hept{\begin{cases}-5\\4\end{cases}}\)

1, \(\sqrt{4-4x+x^2}=3\)
\(\Leftrightarrow\sqrt{\left(2+x\right)^2}=3\)
\(\Leftrightarrow\left|2+x\right|=3\)
TH1: \(\left|2-x\right|=2-x\) với \(2-x\ge0\Leftrightarrow x\le2\)
Pt trở thành:
\(2-x=3\) (ĐK: \(x\le2\) )
\(\Leftrightarrow x=2-3\)
\(\Leftrightarrow x=-1\left(tm\right)\)
TH2: \(\left|2-x\right|=-\left(2-x\right)\) với \(2-x< 0\Leftrightarrow x>2\)
Pt trở thành:
\(-\left(2-x\right)=3\) (ĐK: \(x>2\))
\(\Leftrightarrow-2+x=3\)
\(\Leftrightarrow x=3+2\)
\(\Leftrightarrow x=5\left(tm\right)\)
Vậy \(S=\left\{-1;5\right\}\)
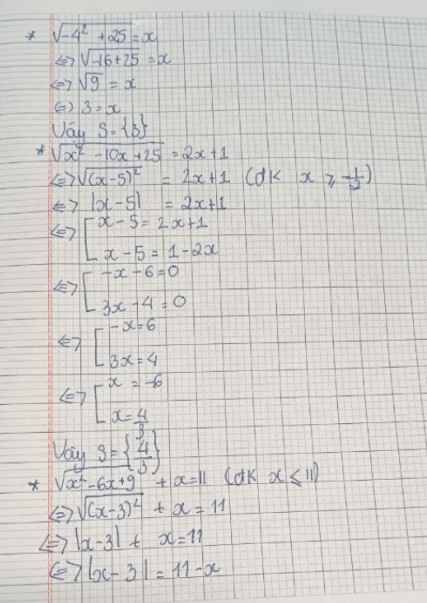
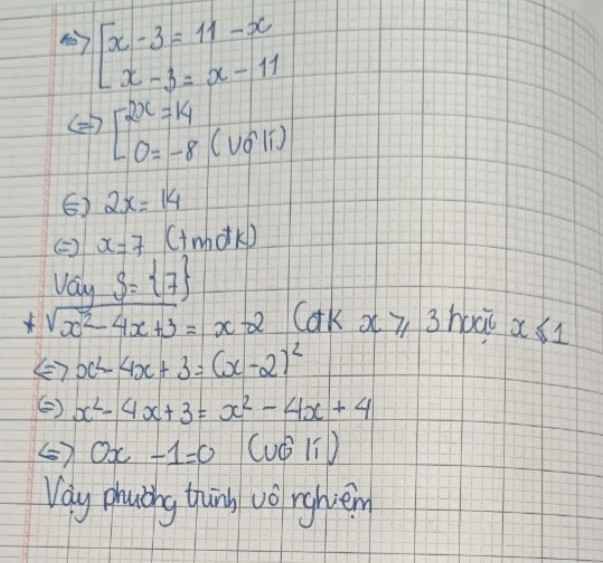
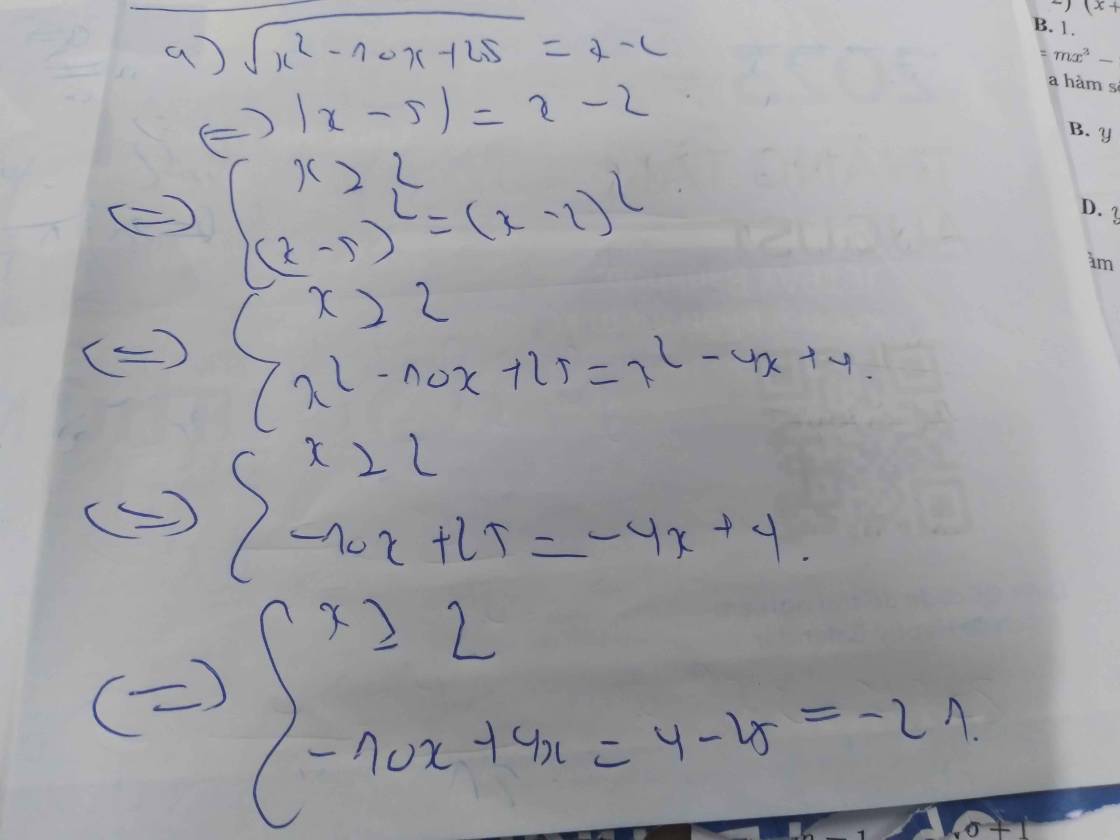
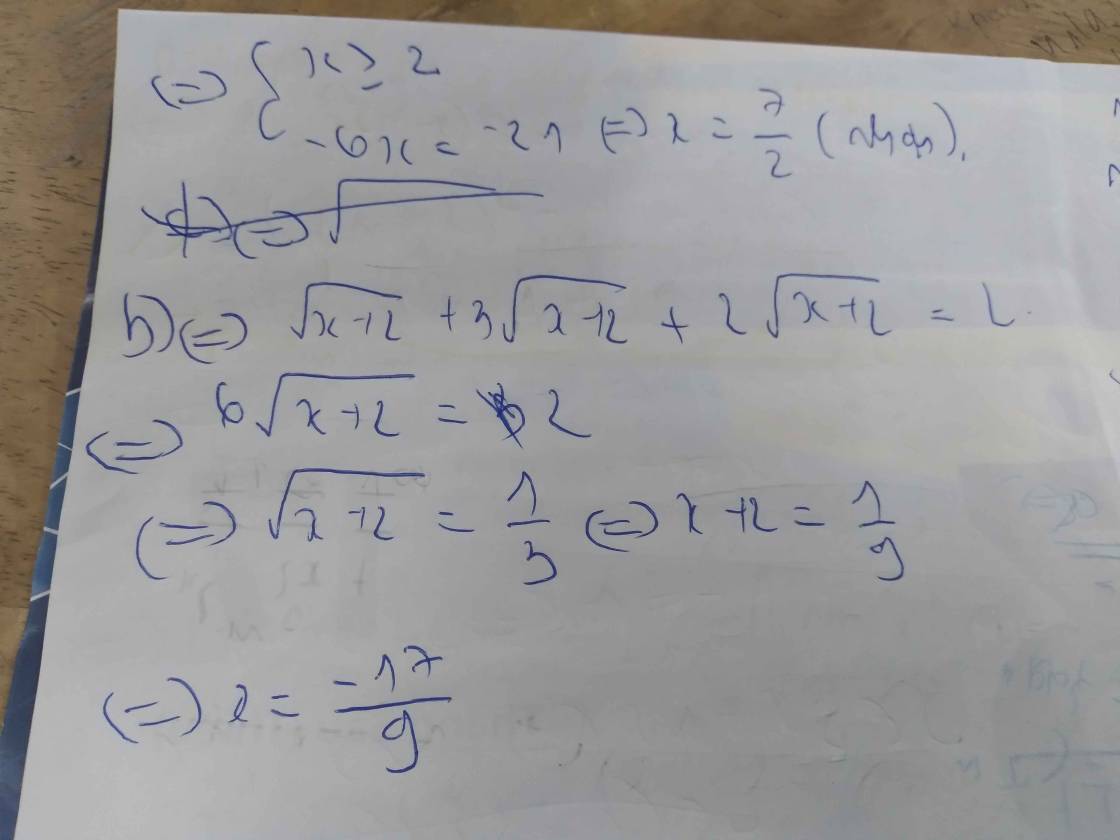
\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=2-x\)
=>\(\left(x-5\right)^2=\left(2-x\right)^2\) và x<=2
=>x^2-10x+25=x^2-4x+4 và x<=2
=>-10x+25=-4x+4 và x<=2
=>-6x=-21 và x<=2
=>x=7/2 và x<=2
=>\(x\in\varnothing\)
\(\sqrt{x^2-10x+25}=2-x\\ < =>\sqrt{\left(x-5\right)^2}=2-x\\ < =>\left|x-5\right|=2-x\)
\(< =>x-5=\left[{}\begin{matrix}2-x\left(x-5\ge0< =>x\ge5\right)\\x-2\left(x-5< 0< =>x< 5\right)\end{matrix}\right.\)
với `x>=5`
`x-5=2-x`
`<=>2x=7`
`<=>x=7/2` (vô lí)
với `x<5`
`x-5=x-2`
`<=>0x=3` (vô lí)
Vậy phương trình vô nghiệm