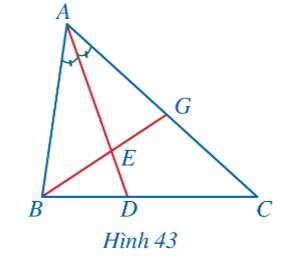
Quan sát Hình 43 và chứng minh \(\frac{{DB}}{{DC}}:\frac{{EB}}{{EG}} = \frac{{AG}}{{AC}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC
28 tháng 2 2020
A B C H D E F
a) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta được:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Xét tam giác ABC có AD là đường phân giác trong của tam giác ABC (gt)
\(\Rightarrow\frac{BD}{DC}=\frac{AB}{AC}\left(tc\right)\)
\(\Rightarrow\frac{BD}{DC}=\frac{3}{4}\)
\(\Rightarrow\frac{BD}{3}=\frac{DC}{4}=\frac{BD+DC}{3+4}\frac{10}{7}\)(tính chất của dãy tỉ số bằng nhau )
\(\Rightarrow\hept{\begin{cases}BD=\frac{10}{7}.3=\frac{30}{7}\left(cm\right)\\DC=\frac{10}{7}.4=\frac{40}{7}\left(cm\right)\end{cases}}\)
b)Ta có: \(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}AH.BC\)
\(\Rightarrow AB.AC=AH.BC\left(đpcm\right)\)
c) Xét tam giác ADB có DE là đường phân giác trong của tam giác ADB(gt)
\(\Rightarrow\frac{EA}{EB}=\frac{AD}{BD}\left(tc\right)\)
Xét tam giác ADC có DF là đường phân giác trong của tam giác ADC (gt)
\(\Rightarrow\frac{FC}{FA}=\frac{DC}{DA}\left(tc\right)\)
\(\Rightarrow\frac{EA}{EB}.\frac{DB}{DC}.\frac{FC}{FA}=\frac{AD}{BD}.\frac{DB}{DC}.\frac{DC}{DA}=1\left(đpcm\right)\)
QT
1
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
Vì \(\left\{ \begin{array}{l}BC \bot AB'\\B'C' \bot AB'\end{array} \right. \Rightarrow BC//B'C'\)(quan hệ từ vuông góc đến song song).
- Xét tam giác \(AB'C'\) có \(BC//B'C'\) và \(BC\) cắt \(AB';AC'\) lần lượt tại \(B;C\).
Theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AB'}} = \frac{{BC}}{{B'C'}} \Rightarrow \frac{x}{{x + h}} = \frac{a}{{a'}} \Rightarrow xa' = a\left( {x + h} \right) \Leftrightarrow xa' = ax + ah\)
\( \Leftrightarrow xa' - ax = ah \Leftrightarrow x\left( {a' - a} \right) = ah \Leftrightarrow x = \frac{{ah}}{{a' - a}}\) (điều phải chứng minh).
F
5 tháng 7 2020
Tự vẽ hình chỉ bt làm ý a,c, thôi thông cảm T^T
a,Xét ΔHAB và ΔABC
\(\widehat{BHA}=\widehat{BAH}=90^o\)
Góc B chung
\(\Rightarrow\Delta HBA\text{∼ }\Delta ABC\)
c,Xét ΔABC ta có:
BC2=AC2+AB2
BC2=162+122
BC2=400
BC=√400=20cm
Ta có ΔHAB~ΔABC(câu a)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12.16}{20}=9,6cm\)
5 tháng 7 2020
a.Xét \(\Delta HBA\)và \(\Delta ABC\)có
\(\widehat{BHA}=\widehat{BAC}=90^0\)
\(\widehat{B}\) chung
Do đó \(\Delta HBA\)đồng dạng \(\Delta ABC\)\((\)g.g\()\)
b.Từ \(\Delta HBA\)đồng dạng \(\Delta ABC\)
\(\Rightarrow\frac{AH}{AC}=\frac{AB}{BC}\)
\(\Rightarrow AH.BC=AB.AC\)
c.Xét \(\Delta ABC\),có \(\widehat{A}\)=90 độ , theo định lý py -ta -go,ta có
\(BC^2=AB^2+AC^2\)
\(BC^2=12^2+16^2\)
\(BC^2=400\)\(\Rightarrow BC=\sqrt{400}\)
\(BC=20cm\)
Ta có \(\frac{AH}{AC}=\frac{AB}{BC}\Leftrightarrow\frac{AH}{16}=\frac{12}{20}\)
\(\Rightarrow AH=\frac{12\times16}{20}\)
\(\Rightarrow AH=9,6cm\)
Chúc bạn học tốt.Phần d mình chưa giải đc nha
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
a) Vì \(ABCD\) là hình bình hành nên \(AB//CD;AD//BC\)
\( \Rightarrow AB//DG;AB//CG;BK//AD;KC//AD\)
Xét tam giác \(DEG\) có \(AB//DG\), theo hệ quả của định lí Thales ta có:
\(\frac{{AE}}{{EG}} = \frac{{EB}}{{ED}}\) (1)
Xét tam giác \(ADE\) có \(BK//AD\), theo hệ quả của định lí Thales ta có:
\(\frac{{EK}}{{AE}} = \frac{{EB}}{{ED}}\) (2)
Từ (1) và (2) suy ra, \(\frac{{AE}}{{EG}} = \frac{{EK}}{{AE}} \Rightarrow A{E^2} = EG.EK\) (điều phải chứng minh).
b) Xét tam giác \(AED\) có:
\(AD//BK \Rightarrow \frac{{AE}}{{AK}} = \frac{{DE}}{{DB}}\)(3)
Xét tam giác \(AEB\) có
\(AB//BK \Rightarrow \frac{{AE}}{{AG}} = \frac{{BE}}{{BD}}\) (4)
Từ (3) và (4) ta được:
\(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = \frac{{DE}}{{BD}} + \frac{{BE}}{{BD}} = \frac{{BD}}{{BD}} = 1\)
Ta có: \(\frac{{AE}}{{AK}} + \frac{{AE}}{{AG}} = 1 \Rightarrow \frac{1}{{AE}} = \frac{1}{{AK}} + \frac{1}{{AG}}\) (chia cả hai vế cho \(AE\)) (điều phải chứng minh).
1 tháng 2 2018
A B D C E G K a b
a) Vì ABCD là hình bình hành ( gt )
Và K thuộc BC nên
AD // BK Theo hệ quả của định lý Ta-let ta có :
\(\frac{EK}{AE}=\frac{EB}{ED}=\frac{AE}{EG}\Rightarrow\frac{EK}{AE}=\frac{AF}{EG}\Rightarrow AE^2=EK.EG\)
b) Ta có :
\(\frac{AE}{EK}-\frac{DE}{DB};\frac{AE}{AG}=\frac{BE}{BD}\)nên
\(\frac{AE}{AK}+\frac{AE}{AG}-\frac{BE}{BD}+\frac{DE}{DB}-\frac{BD}{BD}-1\Rightarrow\frac{1}{AE}=\frac{1}{AK}+\frac{1}{AG}\)
c) bạn tự làm tiếp mỏi tay quá
6 tháng 6 2019
Giải nốt bài của Pác Hiếu:3
Đặt \(AB=a',AD=b\)
Áp dụng Đ/L Thales vào tam giác ABK,ta có:
\(\frac{BK}{KC}=\frac{AB}{CG}\Rightarrow\frac{a'}{CG}=\frac{BK}{KC}\left(1\right)\)
Áp dụng Đ/L Thales vào tam giác ADG,ta có:
\(\frac{CG}{DG}=\frac{CK}{AD}\Rightarrow\frac{CG}{DG}=\frac{CK}{b}\left(2\right)\)
Nhân vế theo vế của (1);(2) ta có:
\(\frac{BK}{b}=\frac{a'}{DG}\Rightarrow BK\cdot DG=a'b\) không đổi.
Xét tam giác ABC với đường phân giác AD ta có: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) (Tính chất đường phân giác)
Xét tam giác ABG với đường phân giác AE ta có: \(\frac{{EB}}{{EG}} = \frac{{AB}}{{AG}}\)(Tính chất đường phân giác)
\( \Rightarrow \frac{{DB}}{{DC}}:\frac{{EB}}{{EG}} = \frac{{AB}}{{AC}}:\frac{{AB}}{{AG}} = \frac{{AG}}{{AC}}\) (đpcm)