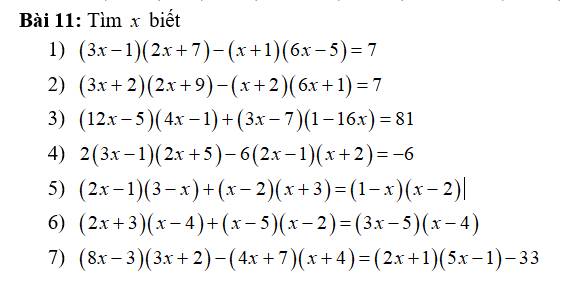
giúp nốt bài này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}=\dfrac{1}{2}\)
nên \(\widehat{B}=60^0\)
b:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=6^2-3^2=27\)
=>\(AC=3\sqrt{3}\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{6}\)
=>\(\dfrac{AD}{1}=\dfrac{CD}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{1}=\dfrac{CD}{2}=\dfrac{AD+CD}{1+2}=\dfrac{3\sqrt{3}}{3}=\sqrt{3}\)
=>\(\left\{{}\begin{matrix}AD=\sqrt{3}\simeq1,7\left(cm\right)\\CD=2\sqrt{3}\simeq3,5\left(cm\right)\end{matrix}\right.\)
c: ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot6=3\cdot3\sqrt{3}=9\sqrt{3}\)
=>\(AH=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
d: ΔABC vuông tại A có AH là đường cao
nên \(BA^2=BH\cdot BC\left(1\right)\)
ΔADB vuông tại A có AE là đường cao
nên \(BE\cdot BD=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BE\cdot BD\)
=>\(\dfrac{BH}{BD}=\dfrac{BE}{BC}\)
Xét ΔBHE và ΔBDC có
BH/BD=BE/BC
\(\widehat{HBE}\) chung
Do đó: ΔBHE đồng dạng với ΔBDC


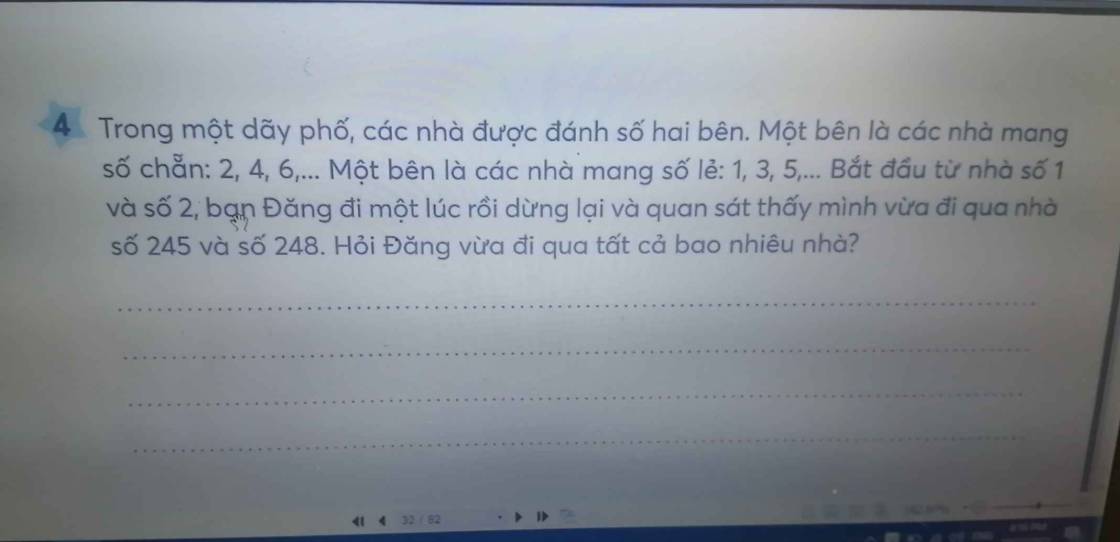
Số căn nhà mang số lẻ bạn Đăng đã đi qua là:
\(\dfrac{245-1}{2}+1=\dfrac{244}{2}+1=122+1=123\left(nhà\right)\)
Số căn nhà mang số chẵn mà bạn Đăng đã đi qua là:
\(\dfrac{248-2}{2}+1=\dfrac{246}{2}+1=123+1=124\left(căn\right)\)
Số căn nhà bạn Đăng đã đi qua là:
123+124=247(căn)

k: \(147\left(19-137\right)-137\left(19-147\right)\)
\(=147\cdot19-147\cdot137-137\cdot19+137\cdot147\)
\(=147\cdot19-137\cdot19\)
\(=19\left(147-137\right)=19\cdot10=190\)
m: \(254\left(195-454\right)-454\left(195-254\right)\)
\(=254\cdot195-254\cdot454-454\cdot195+454\cdot254\)
\(=195\cdot254-195\cdot454\)
\(=195\left(254-454\right)\)
\(=-200\cdot195=-39000\)
n: \(\left(-197\right)\left(24-187\right)-187\cdot\left(197-24\right)\)
\(=-197\cdot24+197\cdot187-187\cdot197+187\cdot24\)
\(=-197\cdot24+187\cdot24\)
\(=24\left(-197+187\right)=24\cdot\left(-10\right)=-240\)
o: \(\left(-248\right)\cdot\left(19-148\right)-148\left(248-19\right)\)
\(=-248\cdot19+248\cdot148-148\cdot248+148\cdot19\)
\(=-19\cdot248+148\cdot19\)
\(=-19\left(248-148\right)\)
\(=-19\cdot100=-1900\)
p: \(\left(-964\right)\left(25+864\right)-864\left(25-964\right)\)
\(=-964\cdot25-964\cdot864-864\cdot25+864\cdot964\)
\(=-964\cdot25-864\cdot25\)
\(=25\cdot\left(-964-864\right)\)
\(=25\left(-1828\right)=-45700\)
q: \(\left(-437\right)\left(17-487\right)-487\cdot\left(437-17\right)\)
\(=-437\cdot17+437\cdot487-487\cdot437+487\cdot17\)
\(=-437\cdot17+487\cdot17\)
\(=17\left(487-437\right)=17\cdot50=850\)




 hứa nốt bài này nữa thuii ạ
hứa nốt bài này nữa thuii ạ 





1: =>6x^2+21x-2x-7-6x^2+5x-6x+5=7
=>18x-2=7
=>18x=9
=>x=1/2
2: (3x+2)(2x+9)-(x+2)(6x+1)=7
=>6x^2+27x-4x-18-6x^2-x-12x-2=7
=>10x-20=7
=>10x=27
=>x=27/10
3: =>48x^2-12x-20x+5+3x-48x^2-7+112x=81
=>83x=83
=>x=1
4: =>2(6x^2+15x-2x-5)-6(2x^2+4x-x-2)=-6
=>12x^2+26x-10-12x^2-18x+12=-6
=>8x+2=-6
=>8x=-8
=>x=-1
5: =>6x-2x^2-3+x+x^2+x-6=-(x^2-3x+2)
=>-x^2+8x-9+x^2-3x+2=0
=>5x-7=0
=>x=7/5
6: =>2x^2-8x+3x-12+x^2-7x+10=3x^2-12x-5x+20
=>3x^2-12x-2=3x^2-17x+20
=>-12x-2=-17x+20
=>5x=22
=>x=22/5
7: =>24x^2+16x-9x-6-4x^2-16x-7x-28=10x^2-2x+5x-1-33
=>20x^2-16x-34=10x^2+3x-34
=>10x^2-19x=0
=>x(10x-19)=0
=>x=0 hoặc x=19/10