tam giác ABC có BC=\(\sqrt{5}\), AC=3 và cotC=2. tính cạnh AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\\CH=\dfrac{12^2}{15}=\dfrac{144}{15}=9,6\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow AH^2=9^2-5.4^2=51,84\)
hay AH=7,2(cm)

a) Để giải tam giác ABC, chúng ta cần biết thêm một thông tin khác về tam giác, ví dụ như độ dài cạnh AC hoặc giá trị của một góc trong tam giác. Với thông tin hiện tại, không đủ để giải tam giác ABC.
b) Từ công thức cotC = AB/BC, và AB = 5cm, ta có:
cotC = 5/BC = 1/3
Vậy, cotC = 1/3.
c) Từ định lý Pythagoras trong tam giác vuông, ta có:
AB^2 + BC^2 = AC^2
8^2 + 15^2 = AC^2
64 + 225 = AC^2
289 = AC^2
AC = √289
AC = 17 cm
Vậy, độ dài cạnh AC của tam giác ABC là 17cm

Vì DE // AC Theo hệ quảTa lét ta có : \(\frac{DB}{AB}=\frac{DE}{AC}\Rightarrow\frac{AB-AD}{AB}=\frac{DE}{AC}\)
\(\Rightarrow\frac{AB-2}{AB}=\frac{2}{AC}\Rightarrow AB.AC-2AC=2AB\)
\(\Rightarrow AB.AC-2\left(AC+AB\right)=0\)(*)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\)(**)
Từ (*) ; (**) ta có hệ : \(\hept{\begin{cases}AB.AC-2\left(AC+AB\right)=0\\AB^2+AC^2=45\end{cases}}\)
bấm casio nhé, mode 9 _ 1 _ ấn hệ ra _ ''=''
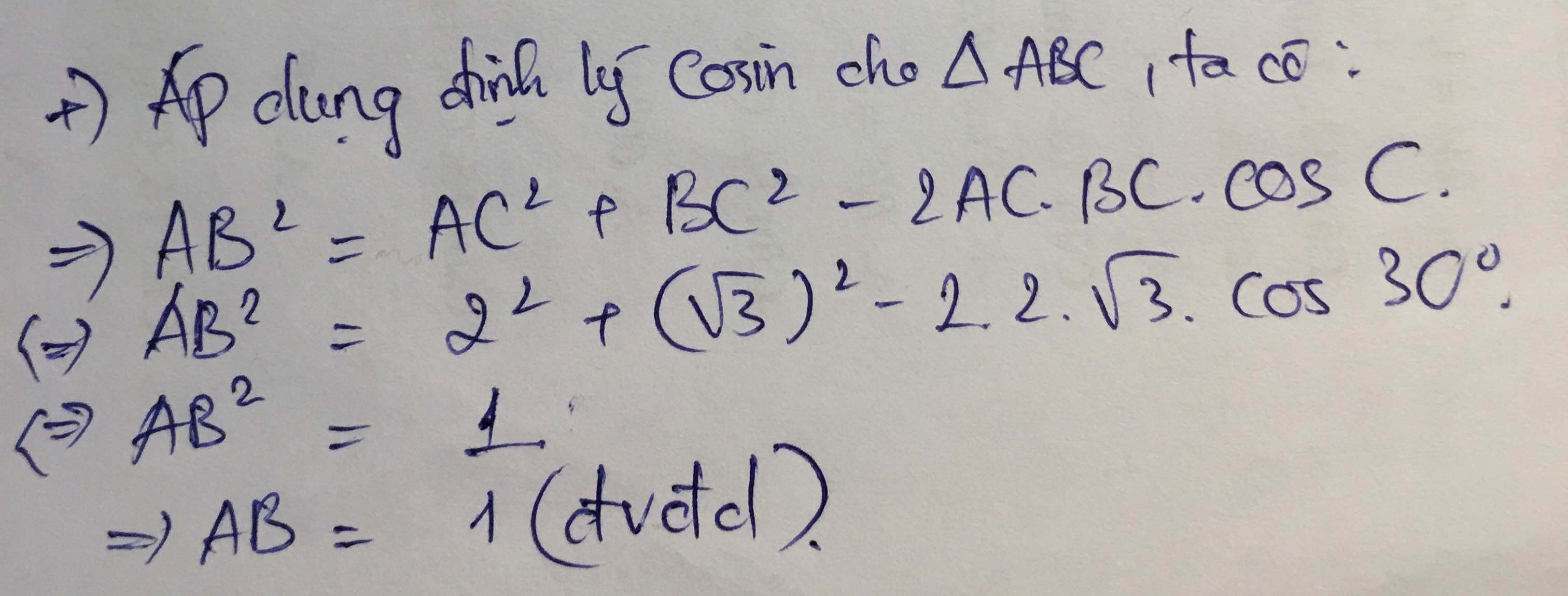
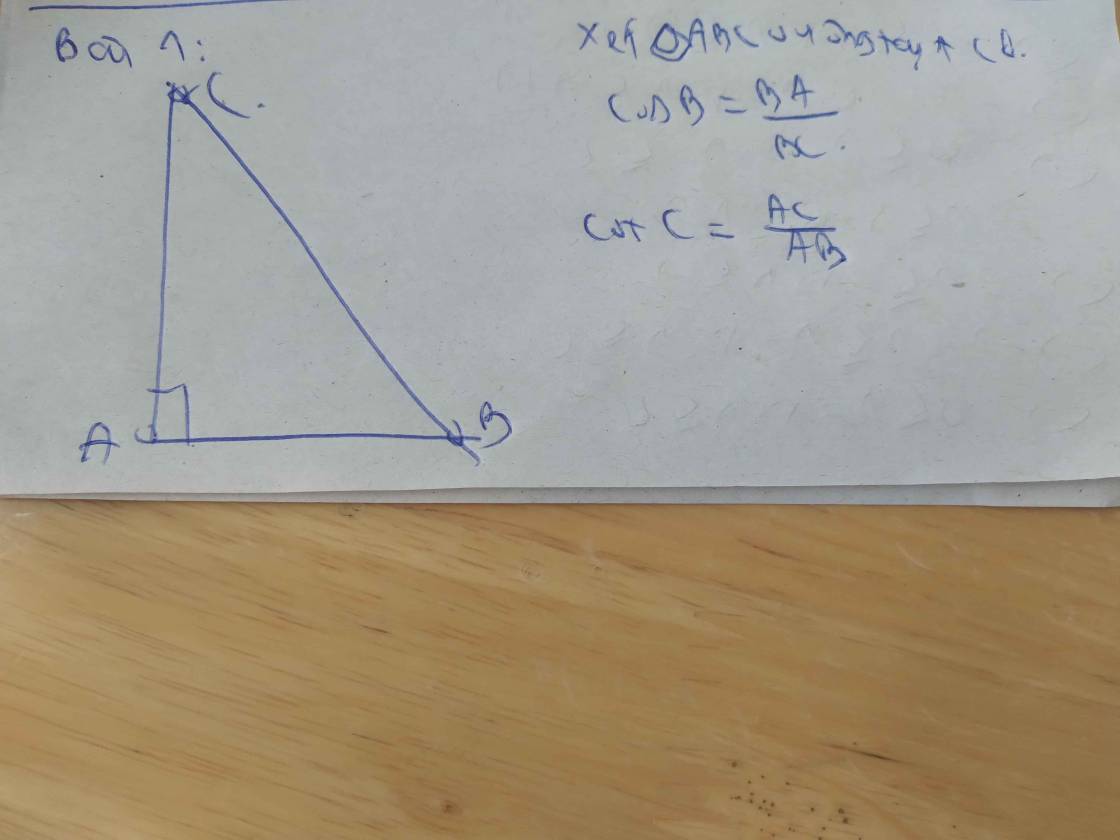

cot C=2
=>\(tanC=\dfrac{1}{cotC}=\dfrac{1}{2}\)
\(1+tan^2C=\dfrac{1}{cos^2C}\)
=>\(cos^2C=1+\dfrac{1}{4}=\dfrac{5}{4}\)
=>\(cosC=\dfrac{2}{\sqrt{5}}\) hoặc \(cosC=-\dfrac{2}{\sqrt{5}}\)
TH1: \(cosC=\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{BC^2+AC^2-AB^2}{2\cdot BC\cdot AB}=\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{5+9-AB^2}{6\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
=>\(14-AB^2=12\)
=>AB^2=2
=>\(AB=\sqrt{2}\)
TH2: \(cosC=-\dfrac{2}{\sqrt{5}}\)
=>\(\dfrac{5+9-AB^2}{6\sqrt{5}}=-\dfrac{2}{\sqrt{5}}\)
=>\(14-AB^2=\dfrac{-2}{\sqrt{5}}\cdot6\sqrt{5}=-12\)
=>AB^2=26
=>\(AB=\sqrt{26}\)