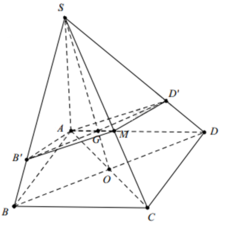
Cho hình chóp SABCD có đáy là hình vuông cạnh a, đường cao SA=2a. Gọi (P) là mặt phẳng qua A và vuông góc với SC. Tính diện tích của hình chóp cắt bởi mặt phẳng (P)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
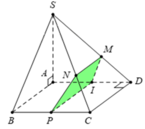
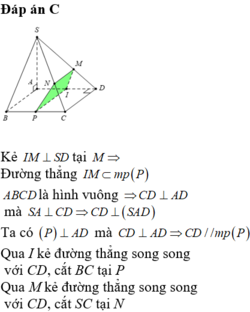
Kẻ I M ⊥ S D tại M Đường thẳng I M ⊂ m p P
ABCD là hình vuông ⇒ C D ⊥ A D mà S A ⊥ C D ⇒ C D ⊥ S A D
Ta có P ⊥ A D mà C D ⊥ A D ⇒ C D / / m p P
Qua I kẻ đường thẳng song song với CD, cắt BC tại P
Qua M kẻ đường thẳng song song với CD, cắt SC tại N
Suy ra mặt phẳng (P) cắt khối chóp S.ABCD theo thiết diện là hình thang vuông IMNP tại M và I.
Tam giác SAD vuông tại A có d A ; S D = a 3 ⇒ I M = a 3 2
Tam giác IMD vuông tại M có M D = I D 2 − I M 2 = a 2 ⇒ S M S D = 7 8 ⇒ M N = 7 a 4
Vậy diện tích hình thang IMNP là S = I M . M N + I P 2 = a 3 2 . 1 2 . 7 a 4 + 2 a = 15 3 16 a 2


Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
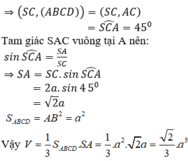

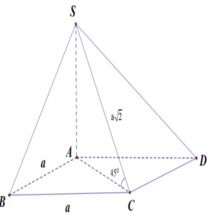
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
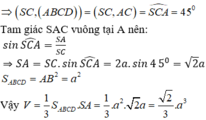

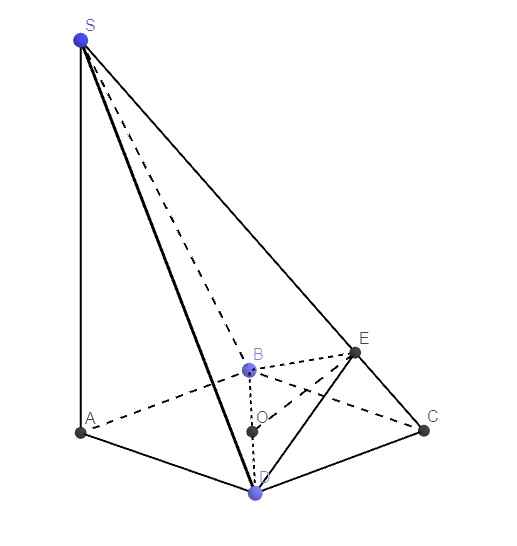
\(\left\{{}\begin{matrix}BD\perp AC\left(\text{ABCD là hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow BD\in\left(\alpha\right)\)
Trong mp (SBC), từ B kẻ \(BE\perp SC\Rightarrow E\in\left(\alpha\right)\)
\(\Rightarrow\) Tam giác BDE là thiết diện của chóp và \(\left(\alpha\right)\)
\(BD=AB\sqrt{2}=a\sqrt{2}\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) hay tam giác SBC vuông tại B
\(SB=\sqrt{SA^2+AB^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{BE^2}=\dfrac{1}{SB^2}+\dfrac{1}{BC^2}-\dfrac{1}{4a^2}+\dfrac{1}{a^2}=\dfrac{5}{4a^2}\Rightarrow BE=DE=\dfrac{2a\sqrt{5}}{5}\)
\(\Rightarrow OE=\sqrt{BE^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{30}}{10}\)
\(S_{BDE}=\dfrac{1}{2}OE.BD=\dfrac{a^2\sqrt{15}}{10}\)
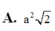
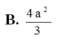
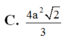
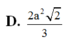


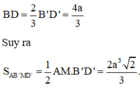
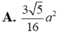
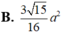
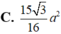




Với thông tin đã cho, ta có Sđ = a^2 và h = SA = 2a. Thay vào công thức, ta có:
Sph = (1/3) * a^2 * 2a = (2/3) * a^3.
Vậy diện tích của hình chóp cắt bởi mặt phẳng (P) là (2/3) * a^3.