Biểu diễn các điểm M(-1;-2), N(-2;-4), P(2;-3), Q(3;-4,5) trên hệ trục tọa độ Oxy. Tìm tọa độ các điểm M', N', P', Q' lần lượt đối xứng với M,N,P,Q qua Ox
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2023
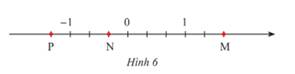
a) Các điểm M, N, Q biểu diễn lần lượt các số hữu tỉ:\(\frac{5}{3};\,\frac{{ - 1}}{3};\,\frac{{ - 4}}{3}\).
b)
CM
11 tháng 4 2018
Đáp án A.
Cách 1: w = 1 + i 3 z + 2 ⇔ z = w − 2 1 + i 3 . Từ đó
z − 1 ≤ 2 ⇔ w − 2 1 + i 3 − 1 ≤ 2 ⇔ w − 3 − i 3 ≤ 2 1 + i 3 ⇔ w − 3 + i 3 ≤ 4
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Cách 2: Gọi w = x + y i ; x , y ∈ ℝ . Khi đó ta có
w = 1 + i 3 z + 2 ⇔ x + y i = 1 + i 3 z + 2 ⇔ x − 2 + y i 1 + i 3 = z
⇒ z − 1 = x − 2 + y i 1 + i 3 − 1 = x − 3 − y − 3 i 1 + i 3 ⇒ z − 1 = x − y 3 + i y − x 3 + 4 3 4
z − 1 ≤ 2 ⇒ x − y 3 2 + y − x 3 + 4 3 2 ≤ 8 ⇒ x − 3 2 + y − 3 2 ≤ 16 .
Vậy tập hợp cần tìm là hình tròn tâm I 3 ; 3 bán kính R = 4 . Chọn đáp án A.
Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w = α z + β trong đó z là số phức tùy ý thỏa mãn z − z 0 ≤ R ( z 0 , α ≠ 0 , β là những số phức cho trước, R là số thực dương cho trước).
Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức α z 0 + β , với bán kính bằng R α .
CM
23 tháng 6 2017
Đáp án A.
Cách 1: w = 1 + i 3 z + 2 ⇔ z = w - 2 1 + i 3 . Từ đó
z - 1 ≤ 2 ⇔ w - 2 1 + i 3 - 1 ≤ 2 ⇔ w - 3 - i 3 ≤ 2 1 + i 3 ⇔ w - 3 + i 3 ≤ 4 .
Vậy tập hợp cần tìm là hình tròn tâm I( 3 ; 3 ) bán kính R = 4. Chọn đáp án A.
Cách 2: Gọi w = x + y i ; x , y ∈ ℝ . Khi đó ta có
w = 1 + i 3 z + 2 ⇔ x + y i = 1 + i 3 z + 2 ⇔ x - 2 + y i 1 + i 3 = z
⇒ z - 1 = x - 2 + y i 1 + i 3 - 1 = x - 3 - y - 3 i 1 + i 3 ⇒ z - 1 = x - y 3 + i y - x 3 + 4 3 4
z - 1 ≤ 2 ⇒ x - y 3 2 + y - x 3 + 4 3 2 ≤ 8 ⇒ x - 3 2 + y - 3 2 ≤ 16 .
Vậy tập hợp cần tìm là hình tròn tâm I( 3 ; 3 ) bán kính R = 4. Chọn đáp án A.
Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w = α z + β trong đó z là số phức tùy ý thỏa mãn z - z 0 ≤ R ( z 0 , α ≢ 0 , β là những số phức cho trước, R là số thực dương cho trước).
Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức α z 0 + β , với bán kính bằng R α .
CM
24 tháng 7 2017
Chọn C.
Gọi M(x;y) là điểm biểu diễn của số phức z = x + yi trên mặt phẳng phức(x, y ∈ R).
Theo đề bài ta có :
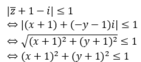
Suy ra, tập hợp các điểm M là hình tròn tâm I(-1;-1) bán kính R = 1 và kể cả đường tròn đó.
M' đối xứng M qua Ox
=>\(\left\{{}\begin{matrix}x_{M'}=-x_M=1\\y_{M'}=y_M=-2\end{matrix}\right.\)
N' đối xứng N qua Ox
=>\(\left\{{}\begin{matrix}x_{N'}=-x_N=2\\y_{N'}=y_N=-4\end{matrix}\right.\)
P' đối xứng P qua Ox
=>\(\left\{{}\begin{matrix}x_{P'}=-x_P=-2\\y_{P'}=y_P=-3\end{matrix}\right.\)
Q' đối xứng Q qua Ox
=>\(\left\{{}\begin{matrix}x_{Q'}=-x_Q=-3\\y_{Q'}=y_Q=-4,5\end{matrix}\right.\)
E chưa hiểu lắm, có thể giải thích được không ạ?