Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mặt phẳng tọa độ Oxy, đồ thị hàm số y = 3/2x - 2 (1) và y = -1/2x + 2 (2). Gọi M là giao điểm của 2 hai đồ thị trên, tìm tọa độ của M
phương trình hoành độ giao điểmM là
3/2x-2=-1/2x+2=>x=2
Tung độ giao điểm M là
y=-1/2.2+2=1
=>M(2;1)
tìm m để đt (d) y= (m-1)x+1 đồng quy với 2 đths (1) và (2)
đt (d) y= (m-1)x+1 đồng quy với 2 đths (1) và (2)
=>đt (d) y= (m-1)x+1 đi qua điểm M(2;1)
=>1=(m-1)2+1=>m=1

Ta biểu diễn các điểm \(M\left( {1;1} \right);N\left( {4;1} \right);P\left( {2; - 1} \right);Q\left( { - 1; - 1} \right)\) trên hệ trục tọa độ ta được:
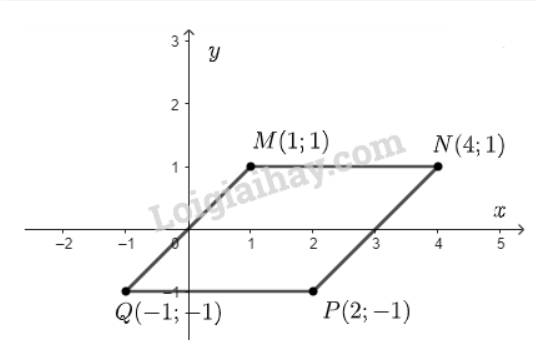
Từ hình vẽ ta thấy, độ dài đoạn thẳng \(MN = 3;QP = 3\)
Lại có: \(MN//Ox;QP//Ox \Rightarrow MN//QP\).
Tứ giác \(MNPQ\) có: \(MN//PQ;MN = PQ \Rightarrow \) tứ giác \(MNPQ\) là hình bình hành.
M' đối xứng M qua Ox
=>\(\left\{{}\begin{matrix}x_{M'}=-x_M=1\\y_{M'}=y_M=-2\end{matrix}\right.\)
N' đối xứng N qua Ox
=>\(\left\{{}\begin{matrix}x_{N'}=-x_N=2\\y_{N'}=y_N=-4\end{matrix}\right.\)
P' đối xứng P qua Ox
=>\(\left\{{}\begin{matrix}x_{P'}=-x_P=-2\\y_{P'}=y_P=-3\end{matrix}\right.\)
Q' đối xứng Q qua Ox
=>\(\left\{{}\begin{matrix}x_{Q'}=-x_Q=-3\\y_{Q'}=y_Q=-4,5\end{matrix}\right.\)
E chưa hiểu lắm, có thể giải thích được không ạ?