hình vuông ABCD có cạnh bằng a. Gọi E là trung điểm cạnh BC, F là trung điểm cạnh AE. Tìm độ dài đoạn thẳng DF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có :
\(\text{AE = DE = }\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{5}}{2}\)
Dùng công thức độ dài trung tuyến:
\(DF^2=\dfrac{DA^2+DE^2}{2}-\dfrac{AE^2}{4}=\dfrac{a^2+\dfrac{5a^2}{4}}{2}-\dfrac{5a^2}{16}=\dfrac{13a^2}{16}\) \(\Rightarrow\) \(DF=\dfrac{a\sqrt{13}}{4}\)

Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)

Đáp án C.
Hướng dẫn giải:
Ta có
![]()
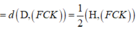
Kẻ H I ⊥ C K , H J ⊥ F I
![]()
Ta có H I = 2 a 5 5
![]()
⇒ S B = a 3
![]()
⇒ H F = a 2 2
Ta có 1 H J 2 = 1 H I 2 + 1 H F 2 = 13 4 a 2
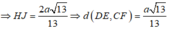
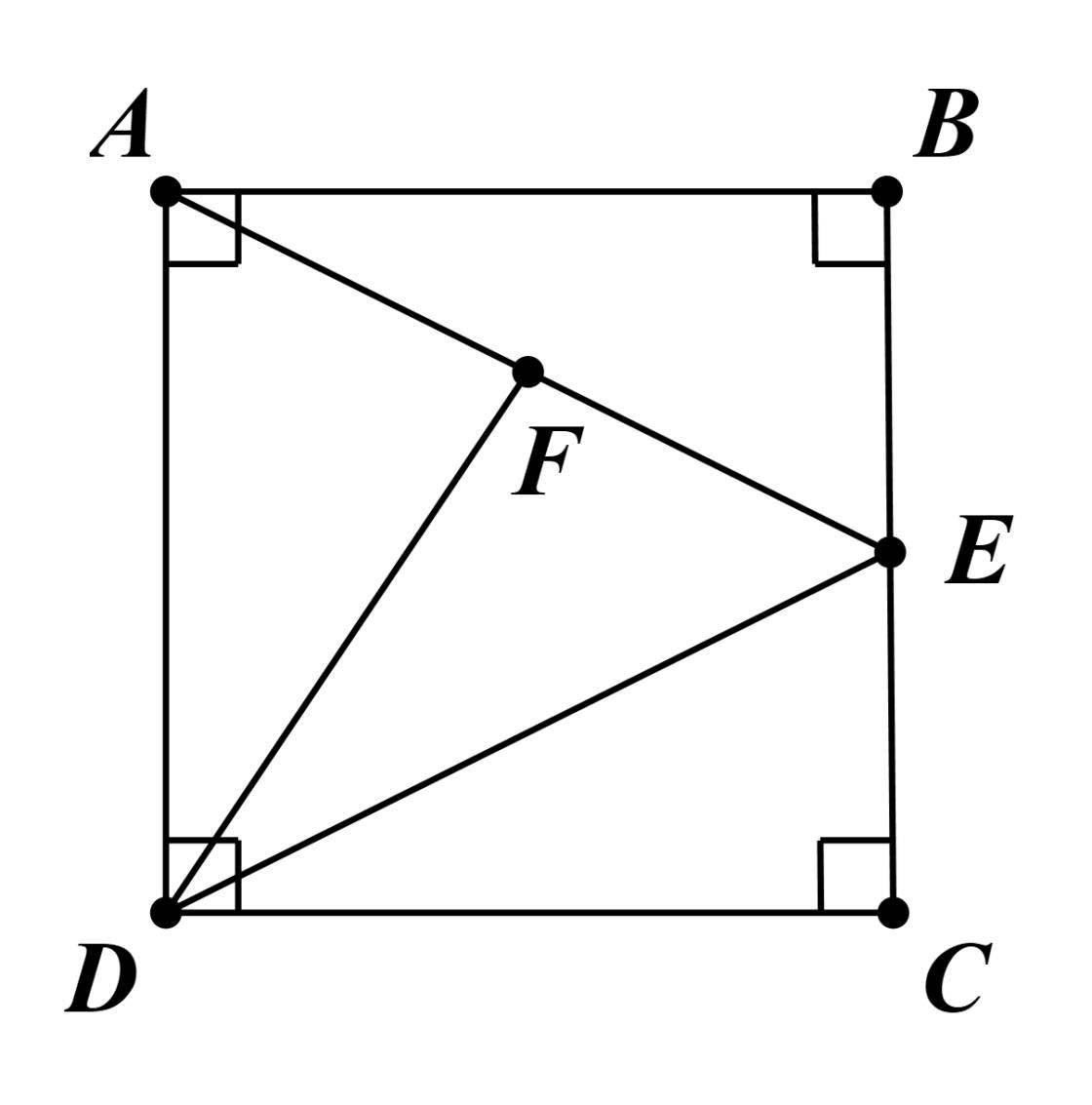
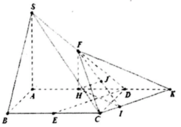
E là trung điểmcủa BC
=>EB=EC=a/2
\(AE=\sqrt{AB^2+BE^2}=\dfrac{a\sqrt{5}}{2}\)
Xét ΔABE vuông tại B có \(\left\{{}\begin{matrix}cosBAE=\dfrac{AB}{AE}=\dfrac{a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{2}{\sqrt{5}}\\sinBAE=\dfrac{BE}{AE}=\dfrac{0.5a}{\dfrac{a\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\end{matrix}\right.\)
=>\(cosDAF=cosBEA=sinBAE=\dfrac{1}{\sqrt{5}}\)
\(AF=\dfrac{AE}{2}=\dfrac{a\sqrt{5}}{4}\)
Xét ΔADF có \(cosDAF=\dfrac{AD^2+AF^2-DF^2}{2\cdot AD\cdot AF}\)
=>\(\dfrac{a^2+a^2\cdot\dfrac{5}{16}-DF^2}{2\cdot\dfrac{a\sqrt{5}}{4}\cdot a}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{\dfrac{21}{16}a^2-DF^2}{\dfrac{a^2\sqrt{5}}{2}}=\dfrac{1}{\sqrt{5}}\)
=>\(\dfrac{21}{16}a^2-DF^2=\dfrac{a^2}{2}\)
=>\(DF^2=\dfrac{13}{16}a^2\)
=>\(DF=\dfrac{a\sqrt{13}}{4}\)