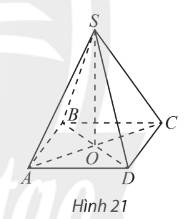
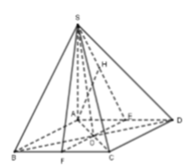
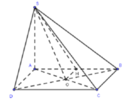
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông với tâm \(O\) và các cạnh bên của hình chóp bằng nhau (Hình 21). Đường thẳng \(SO\) có vuông góc với đáy không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

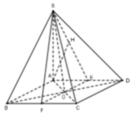
Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF ⇒ AB / / (SEF)
Mà ![]()
![]()
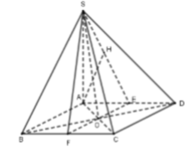
Dựng A H ⊥ S E
Ta thấy: FE / / AB, A B ⊥ ( S A D ) ⇒ F E ⊥ ( S A D ) ⇒ F E ⊥ A H
Mà A H ⊥ S E nên A H ⊥ ( S E F ) ⇔ d ( A , ( S E F ) ) = A H
ABCD là hình vuông cạnh a nên B D = a 2
Dễ dàng chứng minh được ∆ S A B = ∆ S A D c . g . c ⇒ S B = S D
Tam giác SBD cân có S B D = 60 ° nên đều ⇒ S D = B D = a 2
Tam giác SAD vuông tại A có S A = S D 2 - A D 2 = 2 a 2 - a 2 = a
Tam giác SAE vuông tại A có


Do đó
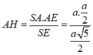
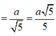
Chọn đáp án D.

Đáp án D
Phương pháp:
- Dựng mặt phẳng chứa SO và song song với AB .
- Sử dụng lý thuyết: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này đến mặt phẳng song song với nó và chứa đường thẳng kia.
- Đưa bài toán về tính khoảng cách từ điểm đến mặt phẳng và kết luận

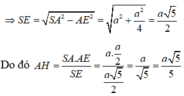

Phương pháp:
- Dựng mặt phẳng chứa SO và song song với AB .
- Sử dụng lý thuyết: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này đến mặt phẳng song song với nó và chứa đường thẳng kia.
- Đưa bài toán về tính khoảng cách từ điểm đến mặt phẳng và kết luận.
Cách giải:
Gọi E, F lần lượt là trung điểm của AD, BC thì AB / / EF => AB / / (SEF)
Mà ![]()
![]()
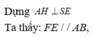
![]()
![]()
![]()
![]()
ABCD là hình vuông cạnh a nên BD = a 2
Dễ dàng chứng minh được ![]()
Tam giác SBD cân có
S
B
D
=
60
0
![]()
Tam giác SAD vuông tại A có ![]()
Tam giác SAE vuông tại A có
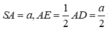
![]()
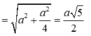
Do đó 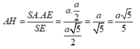
Chọn D.

Đáp án C
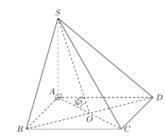
Ta có tam giác SAO vuông cân tạiA.
Suy ra:
S
A
=
O
A
=
A
C
2
=
a
2
2
Vậy : V S . A B C D = 1 3 . S O . S A B C D = a 3 2 6

Đáp án D
Phương pháp:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
Cách giải:
Gọi H là trung điểm của AB => OH//AD
ABCD là hình vuông => AD ⊥ AB; OH ⊥ AB
Mà OH ⊥ SA, (vì SA ⊥ (ABCD))
=> OH ⊥ (SAB)
=>SH là hình chiếu vuông góc của SO trên mặt phẳng (SAB)
=> (SO,(SAB)) = (SO,SH) = HSO
Ta có: OH là đường trung bình của tam giác ABD 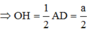
Tam giác SAH vuông tại A ![]()
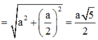
Tam giác SHO vuông tại H: 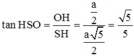


a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
b: Tham khảo:


Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)