Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

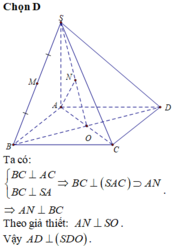
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
b: Tham khảo:


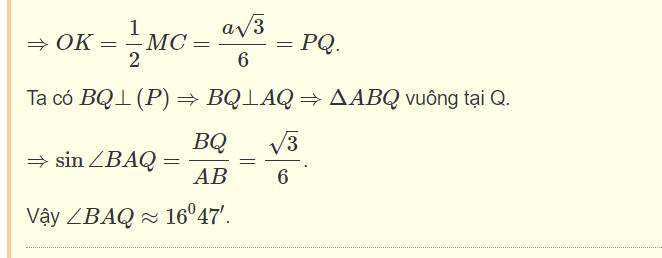

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow\widehat{BSC}\) là góc giữa SC và (SAB)
\(tan\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{\sqrt{10}}{5}\Rightarrow SB=\dfrac{a\sqrt{10}}{2}\)
\(\Rightarrow SA=\sqrt{SB^2-AB^2}=\dfrac{a\sqrt{6}}{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{3}\Rightarrow\widehat{SOA}=60^0\)

Đáp án A.
Gọi H là hình chiếu của C trên SO và góc S O C ^ tù nên H nằm ngoài đoạn SO => CH ⊥ (SBD)
=> Góc tạo bởi SC và (SBD) là C S O ^
Lại có ![]()
![]()
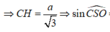
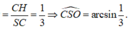

a: DC vuông góc AD
DC vuông góc SA
=>DC vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=căn 3
=>góc SDA=60 độ

Đáp án D
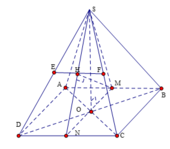
Vì AB//(SCD) => khoảng cách d giữa AB bằng khoảng cách giữa AB và (SCD)
Gọi M, N lần lượt là trung điểm của AB, CD khi đó AB ⊥ (SMN)
Kẻ đường cao MH của ∆ SMN => MH là khoảng cách giữa AB và SC
Ta có:
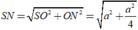
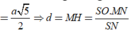
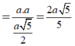

Đáp án D
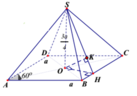
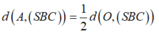
AC cắt (SBC) tại C , O là trung điểm AC =>khoảng cách
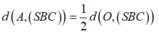
* Trong (ABCD) dựng OH ⊥ BC, trong (SOH) dựng OK ⊥ SH ta chứng minh được OK ⊥ (SBC)
=> khoảng cách d(O,(SBC))= OK.
∆ O B C vuông tại O có OH đường cao
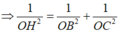
∆ S O H vuông tại O có OK đường cao
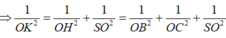
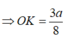
Vậy
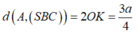
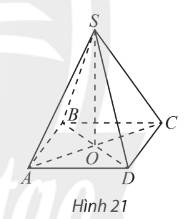
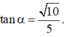


Tam giác \(SAC\) cân tại \(S \Rightarrow SO \bot AC\)
Tam giác \(SB{\rm{D}}\) cân tại \(S \Rightarrow SO \bot B{\rm{D}}\)
\( \Rightarrow SO \bot \left( {ABCD} \right)\)