Question

[Phạm Hoàng Tiến]

Giúp mình câu 20  được không ạ:))

Answer 1

[Nguyễn Lê Phước Thịnh]

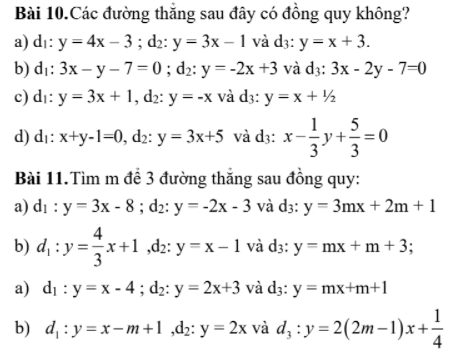
20:

a: 5JB=2JC

=>JB/2=JC/5

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{JC}{5}=\dfrac{JB}{2}=\dfrac{JC-JB}{5-2}=\dfrac{BC}{3}\)

=>JC=5/3*BC; JB=2/3BC

2CI=3BI

=>CI/3=BI/2=(CI+BI)/(3+2)=CB/5

=>CI=3/5CB; BI=2/5CB

\(\overrightarrow{AI}=\overrightarrow{AB}+\overrightarrow{BI}\)

=\(\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BC}\)

\(=\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}=\dfrac{3}{5}\overrightarrow{AB}+\dfrac{2}{5}\overrightarrow{AC}\)

\(\overrightarrow{AJ}=\overrightarrow{AB}+\overrightarrow{BJ}\)

\(=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{BC}\)

\(=\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{BA}-\dfrac{2}{3}\overrightarrow{AC}\)

\(=\dfrac{5}{3}\overrightarrow{AB}-\dfrac{2}{3}\overrightarrow{AC}\)

b: Gọi giao của AG với BC là M

=>M là trung điểm của BC

Xét ΔABC có

G là trọng tâm

AM là đường trung tuyến

=>\(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}=\dfrac{2}{3}\cdot\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)

Đặt \(\overrightarrow{AG}=x\cdot\overrightarrow{AI}+y\cdot\overrightarrow{AJ}\)

=>\(\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}=\dfrac{3}{5}\cdot x\cdot\overrightarrow{AB}+\dfrac{2}{5}\cdot x\cdot\overrightarrow{AC}+\dfrac{5}{3}\cdot y\cdot\overrightarrow{AB}-\dfrac{2}{3}\cdot y\cdot\overrightarrow{AC}\)

Đồng nhất hệ số, ta được hệ phương trình:

3/5x+5/3y=1/3 và 2/5x-2/3y=1/3

=>x=35/48 và y=-1/16

=>\(\overrightarrow{AG}=\dfrac{35}{48}\overrightarrow{AI}-\dfrac{1}{16}\overrightarrow{AJ}\)