Câu 3. Không thực hiện phép tính, chứng minh rằng 𝐶 = 111111.18 𝑐ℎ𝑖𝑎 ℎế𝑡 𝑐ℎ𝑜...
Đọc tiếp
Câu 3. Không thực hiện phép tính, chứng minh rằng 𝐶 = 111111.18 𝑐ℎ𝑖𝑎 ℎế𝑡 𝑐ℎ𝑜 27
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(B=2024\cdot14\)
\(B=2\cdot1012\cdot14\)
\(B=28\cdot1012\)
Vậy B chia hết cho 28
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(11^{2024}\)
\(=11^2\cdot11^{2022}\)
\(=121\cdot11^{2022}\)
Vậy \(11^{2024}\) chia hết cho \(121\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(3^{2022}\)
\(=3^2\cdot3^{2020}\)
\(=3^2\cdot3^2\cdot3^{2018}\)
\(=3^4\cdot3^{2018}\)
\(=81\cdot3^{2018}\)
Vậy \(3^{2022}\) chia hết cho 81
PT
1
NV
1
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
Ta có:
\(A=15\cdot16\)
\(A=3\cdot5\cdot2^4\)
\(A=3\cdot5\cdot2^3\cdot2\)
\(A=2^3\cdot5\cdot3\cdot2\)
\(A=40\cdot6\)
Vậy A chia hết cho 40
KV
6 tháng 11 2023
A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... 2¹⁶) ⋮ 5
Vậy A ⋮ 5
LT
1
3 tháng 7 2017
1995*1997-1/1996*1995+1994
=1995*(1996+1)-1/1996*1995+1994
=1995*1996+1995-1/1996*1995+1994
=1995*1996+1994/1996*1995+1994
=1
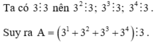
Ta có:
\(C=111111\cdot18\)
\(C=3\cdot7\cdot11\cdot13\cdot37\cdot3^2\cdot2\)
\(C=\left(3\cdot3^2\right)\cdot\left(7\cdot11\cdot13\cdot37\cdot2\right)\)
\(C=3^3\cdot74074\)
\(C=27\cdot74074\)
Vậy C chia hết cho 27