Cho hình chóp đều \(S.ABC\). Gọi \(A',B',C'\) lần lượt là trung điểm của các đoạn thẳng \(SA,SB,SC\). Chứng minh rằng phần hình chóp đã cho giới hạn bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) là hình chóp cụt đều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


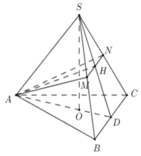
Chọn B.
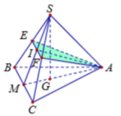
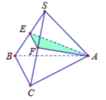
Gọi M là trung điểm BC, I = EF ∩ SM, suy ra I là trung điểm EF và SM.
Có ![]() => AF = AE => AEF cân tại A => AI
⊥
EF.
=> AF = AE => AEF cân tại A => AI
⊥
EF.
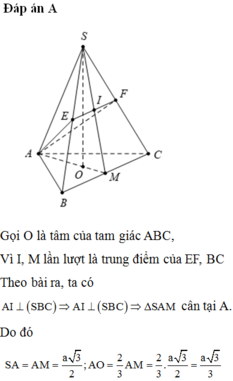
Tam giác ASM có AI ⊥ SM và I là trung điểm SM nên ASM cân tại A, suy ra SA = AM = a 3 2 .
Gọi G là trọng tâm tam giác ABC ![]()
Trong tam giác SAG có: 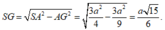
Vậy thể tích khối chóp S.ABC là ![]()

Đáp án A
Hướng dẫn giải:
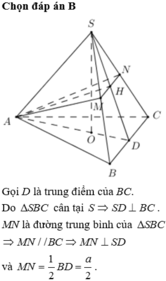
Gọi G là trọng tâm tam giác đều ABC và M là trung điểm AB
Khi đó S G ⊥ ( A B C )
Do A B ⊥ S G A B ⊥ C M ⇒ A B ⊥ H M
Lại có C M = a 3 2

⇒ S G = a 11 3
Suy ra H M = S G . C M S C = a 11 4 .
⇒ C H = C M 2 - H M 2 = a 4
Khi đó S H = 7 a 4
⇒ V = 1 3 S H . S H B C = 7 a 3 11 96

Đáp án A
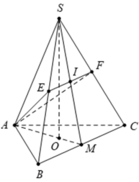
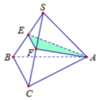
Gọi O là tâm của tam giác ABC, Vì I, M lần lượt là trung điểm của EF, BC
Theo bài ra, ta có ![]() cân tại A
cân tại A
Do đó 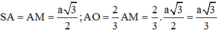
![]()
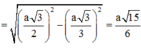
Vậy 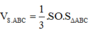
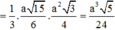
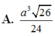
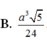
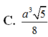
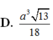



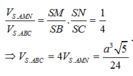

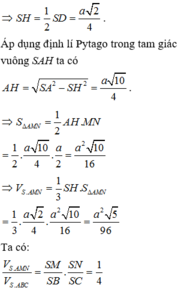
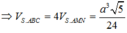




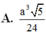
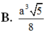
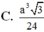
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của \(\Delta SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(\left. \begin{array}{l}A'B'\parallel \left( {ABC} \right)\\A'C'\parallel \left( {ABC} \right)\\A'B',A'C' \subset \left( {A'B'C'} \right)\end{array} \right\} \Rightarrow \left( {A'B'C'} \right)\parallel \left( {ABC} \right)\)
Vậy phần hình chóp đã cho giới hạn bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) là hình chóp cụt đều.