Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\begin{array}{l}\left. \begin{array}{l}A \in \left( {ABC} \right)\\B \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AB \subset \left( {ABC} \right)\\\left. \begin{array}{l}B \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow BC \subset \left( {ABC} \right)\\\left. \begin{array}{l}A \in \left( {ABC} \right)\\C \in \left( {ABC} \right)\end{array} \right\} \Rightarrow AC \subset \left( {ABC} \right)\end{array}\)
\(SA \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow SA\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SB \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow SB\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(SC \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow SC\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow A'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(A'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow A'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow B'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(B'C \cap \left( {ABC} \right) = \left\{ C \right\} \Rightarrow B'C\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'A \cap \left( {ABC} \right) = \left\{ A \right\} \Rightarrow C'A\) cắt mặt phẳng \(\left( {ABC} \right)\).
\(C'B \cap \left( {ABC} \right) = \left\{ B \right\} \Rightarrow C'B\) cắt mặt phẳng \(\left( {ABC} \right)\).
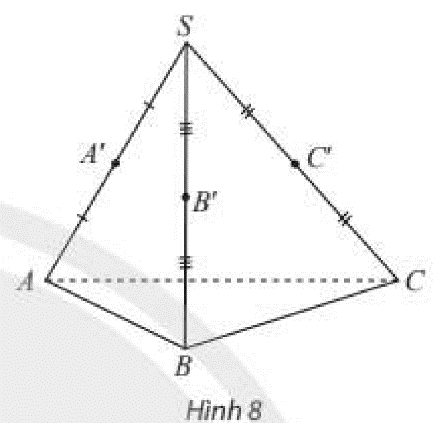
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(B'\) là trung điểm của \(SB\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow B'C'\) là đường trung bình của tam giác \(SBC\)
\(\left. \begin{array}{l} \Rightarrow B'C'\parallel BC\\BC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow B'C'\parallel \left( {ABC} \right)\)

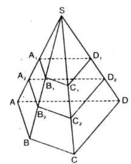
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
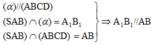
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
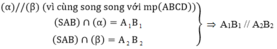
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D

SA vuông góc (P)
SA vuông góc (ABC)
=>(P)//(ABC)
=>B'C'//BC

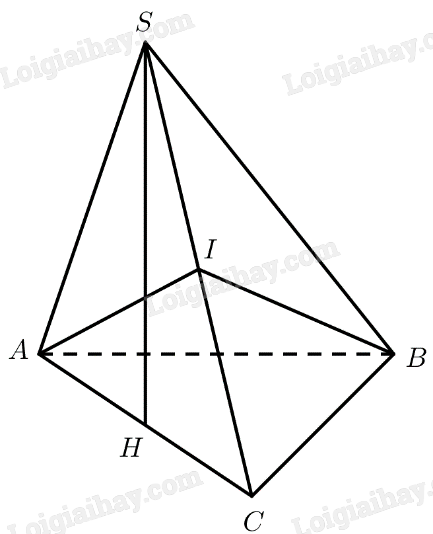
a) Gọi \(H\) là trung điểm của \(AC\)
\(SAC\) là tam giác đều \( \Rightarrow SH \bot AC\)
Mà \(\left( {SAC} \right) \bot \left( {ABC} \right)\)
\( \Rightarrow SH \bot \left( {ABC} \right) \Rightarrow SH \bot BC\)
Lại có \(AC \bot BC\)
\(\left. \begin{array}{l} \Rightarrow BC \bot \left( {SAC} \right)\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow \left( {SBC} \right) \bot \left( {SAC} \right)\)
b) \(SAC\) là tam giác đều \( \Rightarrow AI \bot SC\)
\(BC \bot \left( {SAC} \right) \Rightarrow BC \bot AI\)
\(\left. \begin{array}{l} \Rightarrow AI \bot \left( {SBC} \right)\\AI \subset \left( {ABI} \right)\end{array} \right\} \Rightarrow \left( {ABI} \right) \bot \left( {SBC} \right)\)

Kẻ \(SH\perp\left(ABC\right)\) \(\Rightarrow\widehat{SAH}=60^0\)
Áp dụng hệ thức lượng vào tam giác vuông có:
\(tan60^0=\dfrac{SH}{SA}\Leftrightarrow SH=\sqrt{3}a\)
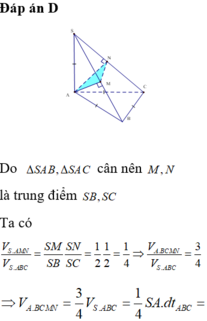
Ta có M và N lần lượt là trung điểm của SA và SB
\(\Rightarrow\) MN là đường trung bình của tam giác ABC
\(\Rightarrow MN//BC\)
mà \(BC\subset\left(ABC\right)\) , \(MN⊄(ABC) \)
\(\Rightarrow MN//\left(ABC\right)\)
\(d\left(MN,\left(ABC\right)\right)=d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)=\dfrac{\sqrt{3}}{2}.a\)
Vậy \(d\left(MN,\left(ABC\right)\right)=\dfrac{\sqrt{3}}{2}a\)
Chứng minh \(d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)\)
Kẻ \(MK\perp\left(ABC\right)\Rightarrow MK//SH\)
Áp dụng định lý thales: \(\dfrac{MK}{SH}=\dfrac{AM}{AS}=\dfrac{1}{2}\)
\(\Rightarrow MK=\dfrac{1}{2}SH\Rightarrow d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)\) (đpcm)

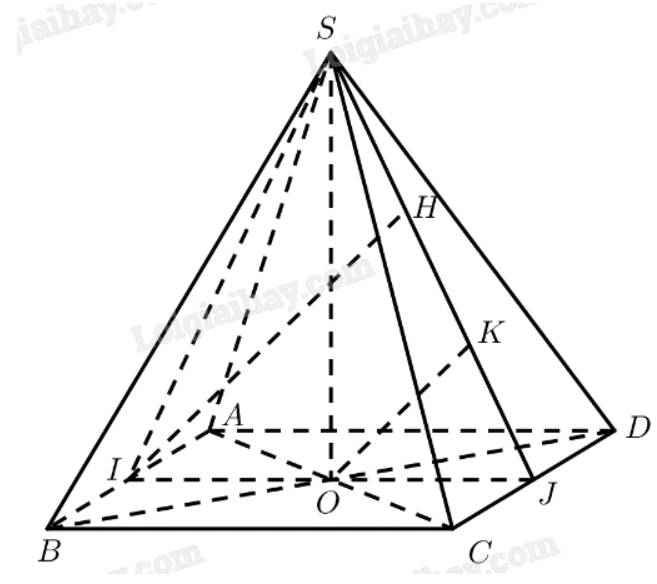
a) Gọi \(O\) là tâm của đáy
\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AB\)
\(I\) là trung điểm của \(AB\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow IJ\) là đường trung bình của hình vuông \(ABCD\)
\(\left. \begin{array}{l} \Rightarrow IJ\parallel A{\rm{D}}\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow IJ \bot AB\)
Ta có:
\(\left. \begin{array}{l}SO \bot AB\\IJ \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {SIJ} \right)\)
b) Kẻ \(IH \bot SJ\left( {H \in SJ} \right),OK \bot SJ\left( {K \in SJ} \right) \Rightarrow IH\parallel OK\)
\(O\) là trung điểm của \(IJ \Rightarrow IH = 2{\rm{O}}K\)
Ta có:
\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {AB,SC} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}\left. \begin{array}{l}AB \bot \left( {SIJ} \right)\\C{\rm{D}}\parallel AB\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SIJ} \right) \Rightarrow C{\rm{D}} \bot IH\\ & IH \bot SJ\end{array} \right\} \Rightarrow IH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {AB,C{\rm{D}}} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right) = IH\end{array}\)
\(O\) là trung điểm của \(IJ\), \(IH\parallel {\rm{O}}K\)\( \Rightarrow IH = 2{\rm{O}}K\)
\(O\) là trung điểm của \(B{\rm{D}}\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow OJ\) là đường trung bình của \(\Delta BCD\)
\( \Rightarrow OJ = \frac{1}{2}BC = \frac{a}{2}\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O\)\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \frac{{a\sqrt 6 }}{2}\)
\(\Delta SOJ\) vuông tại \(O\) có đường cao \(OK\)
\( \Rightarrow OK = \frac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }} = \frac{{a\sqrt {42} }}{{14}}\)
\( \Rightarrow d\left( {AB,C{\rm{D}}} \right) = IH = 2OK = \frac{{a\sqrt {42} }}{7}\)
\(A'\) là trung điểm của \(SA\)
\(B'\) là trung điểm của \(SB\)
\( \Rightarrow A'B'\) là đường trung bình của \(\Delta SAB\)
\(\left. \begin{array}{l} \Rightarrow A'B'\parallel AB\\AB \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'B'\parallel \left( {ABC} \right)\)
\(A'\) là trung điểm của \(SA\)
\(C'\) là trung điểm của \(SC\)
\( \Rightarrow A'C'\) là đường trung bình của \(\Delta SAC\)
\(\left. \begin{array}{l} \Rightarrow A'C'\parallel AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow A'C'\parallel \left( {ABC} \right)\)
\(\left. \begin{array}{l}A'B'\parallel \left( {ABC} \right)\\A'C'\parallel \left( {ABC} \right)\\A'B',A'C' \subset \left( {A'B'C'} \right)\end{array} \right\} \Rightarrow \left( {A'B'C'} \right)\parallel \left( {ABC} \right)\)
Vậy phần hình chóp đã cho giới hạn bởi hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {A'B'C'} \right)\) là hình chóp cụt đều.