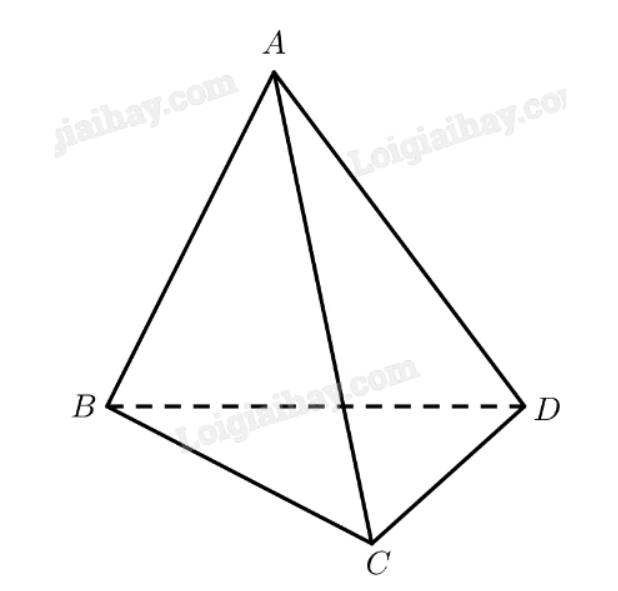
Cho tứ diện ABCD có \(AB \bot (BCD),BC \bot CD\). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
a) \(CD \bot BM\)
b, \(BM \bot MN\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có H là trực tâm của tam giác BCD \( \Rightarrow BH \bot CD\left( 2 \right)\)
Tử (1) và (2) \( \Rightarrow CD \bot \left( {ABH} \right)\)
b) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\left( 1 \right)\)
Có K là trực tâm của tam giác BCD \( \Rightarrow AK \bot CD\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CD \bot \left( {ABK} \right)\)
21 tháng 8 2023
tham khảo:
a) Tam giác ABD có HK là đường trung bình nên HK//BD
Vì ABCD là hình vuông nên AC⊥BD. Suy ra AC⊥HK
Vì SH⊥(ABCD) nên SH⊥AC
Ta có: AC⊥SH,AC⊥HK nên AC⊥(SHK)
b) Ta có tam giác AHD và tam giác DKC bằng nhau nên DH⊥CK
Mà SH⊥(ABCD) nên SH⊥CK
Suy ra CK⊥(SDH)
21 tháng 8 2023
tham khảo:
a) Tam giác SAB có MN là đường trung bình nên MN//SA
Mà SA⊥(ABCD) nên MN⊥(ABCD). Suy ra MN⊥AB
Hình thang ABCD có NP là đường trung bình nên NP//BC//AD. Mà BC⊥AB nên NP⊥ABTa có AB vuông góc với hai đường thẳng MN và NP cắt nhau cùng thuộc (MNPQ) nên AB⊥(MNPQ)
b) Vì AB⊥(MNPQ);MQ∈(MNPQ) nên AB⊥MQ
Tam giác SBC có MQ là đường trung bình nên MQ//BC. Mà SA⊥BC nên SA⊥MQ
Ta có MQ vuông góc với hai đường thẳng SA và AB cắt nhau cùng thuộc (SAB) nên MQ⊥(SAB)
21 tháng 8 2023
tham khảo:
a) Vì SA⊥(ABCD) nên SA⊥CD
Ta có: DC⊥AD;DC⊥SA nên DC⊥(SAD)
b) Vì SA⊥(ABCD) nên SA⊥CM
Ta có: AB = 2CD nên AM = CD. Suy ra AMCD là hình chữ nhật nên CM⊥AB
Mà CM⊥SA
Suy ra: CM⊥(SAB)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Ta có:
\(\left. \begin{array}{l}\left( {ABD} \right) \bot \left( {BCD} \right)\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\C{\rm{D}} \subset \left( {BCD} \right)\\C{\rm{D}} \bot B{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABD} \right) \Rightarrow C{\rm{D}} \bot A{\rm{D}}\)
Vậy tam giác \(ACD\) vuông tại \(D\).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
.png)
\(\begin{array}{l}\left. \begin{array}{l} + )BC \bot AB\left( {hcn\,\,ABCD} \right)\\BC \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AB \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAB} \right);AM \subset \left( {SAB} \right) \Rightarrow BC \bot AM\\\left. \begin{array}{l} + )CD \bot AD\left( {hcn\,\,ABCD} \right)\\CD \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)\\AD \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow CD \bot \left( {SAD} \right);AN \subset \left( {SAD} \right) \Rightarrow CD \bot AN\end{array}\)
\(\begin{array}{l}\left. \begin{array}{l} + )AM \bot SB\\AM \bot BC\\SB \cap BC = \left\{ B \right\}\end{array} \right\} \Rightarrow AM \bot \left( {SBC} \right);SC \subset \left( {SBC} \right) \Rightarrow SC \bot AM\\\left. \begin{array}{l} + )AN \bot SD\\AN \bot CD\\SD \cap CD = \left\{ D \right\}\end{array} \right\} \Rightarrow AN \bot \left( {SCD} \right);SC \subset \left( {SCD} \right) \Rightarrow SC \bot AN\\\left. \begin{array}{l} + )AM \bot SC\\AN \bot SC\\AM \cap AN = \left\{ A \right\}\end{array} \right\} \Rightarrow SC \bot \left( {AMN} \right)\end{array}\)
21 tháng 8 2023
tham khảo:
a) Tam giác AOB có A'B' là đường trung bình nên A'B'//AB hay A'B'//(OBC)
Tam giác AOC có A'C' là đường trung bình nên A'C"//AC hay A'C'//(OBC)
Suy ra (A'B'C')//(OBC)
Mà OA⊥(OBC) nên OA⊥(A′B′C′)
b) Vì OA⊥(OBC);BC∈(OBC) nên OA⊥CB
Ta có đường thẳng BC vuông góc với hai đường thẳng OH và OA cắt nhau cùng thuộc (AOH) nên BC⊥(OAH)
Mà tam giác ABC có B'C' là đường trung bình nên B'C'//BC
Suy ra B′C′⊥(AOH)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
\(\begin{array}{l}\left. \begin{array}{l} + )AC \bot BD\,\,\left( {hv\,\,ABCD} \right)\\SA \bot BD\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} + )BD \bot SC\left( {BD \bot \left( {SAC} \right)} \right)\\BM \bot SC\\BD \cap BM = \left\{ B \right\}\end{array} \right\} \Rightarrow SC \bot \left( {MBD} \right)\end{array}\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
\(\left. \begin{array}{l}SC \bot \left( {MBD} \right)\\OM \subset \left( {MBD} \right)\end{array} \right\} \Rightarrow SC \bot OM\)
Mà \(AH \bot SC\)
\( \Rightarrow AH//OM,OM \subset \left( {MBD} \right) \Rightarrow AH//\left( {MBD} \right)\)
22 tháng 9 2023
Gọi \(I = CN \cap DM\)
\(\Delta SAB\) đều \( \Rightarrow SM \bot AB\)
Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right),\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\)
\( \Rightarrow SM \bot \left( {ABCD} \right) \Rightarrow SM \bot CN\)
\(\Delta A{\rm{D}}M = \Delta DCN\left( {c.g.c} \right) \Rightarrow \widehat {AM{\rm{D}}} = \widehat {CN{\rm{D}}}\)
Mà \(\widehat {AM{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ }\)
\(\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M} = {90^ \circ } \Rightarrow \widehat {NI{\rm{D}}} = {180^ \circ } - \left( {\widehat {CN{\rm{D}}} + \widehat {A{\rm{D}}M}} \right) = {90^ \circ } \Rightarrow CN \bot DM\)
\(\left. \begin{array}{l}\left. \begin{array}{l}SM \bot CN\\CN \bot DM\end{array} \right\} \Rightarrow CN \bot \left( {SM{\rm{D}}} \right)\\CN \subset \left( {SNC} \right)\end{array} \right\} \Rightarrow \left( {SNC} \right) \bot \left( {SM{\rm{D}}} \right)\)
b) Kẻ \(MH \bot SI\left( {H \in SI} \right)\)
\(CN \bot \left( {SM{\rm{D}}} \right) \Rightarrow CN \bot MH\)
\( \Rightarrow MH \bot \left( {SNC} \right) \Rightarrow d\left( {M,\left( {SNC} \right)} \right) = MH\)
\(\Delta C{\rm{D}}N\) vuông tại \(D\) có đường cao \(DI\)
\(DN = \frac{1}{2}A{\rm{D}} = \frac{a}{2},CN = \sqrt {C{{\rm{D}}^2} + D{N^2}} = \frac{{a\sqrt 5 }}{2},DI = \frac{{C{\rm{D}}.DN}}{{CN}} = \frac{{a\sqrt 5 }}{5}\)
\(DM = CN = \frac{{a\sqrt 5 }}{2} \Rightarrow MI = DM - DI = \frac{{3a\sqrt 5 }}{{10}}\)
\(\Delta SAB\) đều \( \Rightarrow SM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta SMI\) vuông tại \(M\) có đường cao \(MH\)
\( \Rightarrow MH = \frac{{SM.MI}}{{\sqrt {S{M^2} + M{I^2}} }} = \frac{{3a\sqrt 2 }}{8}\)
Vậy \(d\left( {M,\left( {SNC} \right)} \right) = \frac{{3a\sqrt 2 }}{8}\)
a) Vì \(AB \bot \left( {BCD} \right) \Rightarrow AB \bot CD\)
Mà \(CD \bot BC\)\( \Rightarrow CD \bot \left( {ABC} \right)\)
Lại có \(BM \in \left( {ABC} \right)\)\( \Rightarrow CD \bot BM\)
b) Ta có \(\left. \begin{array}{l}BM \bot CD\\BM \bot AC\end{array} \right\} \Rightarrow BM \bot \left( {ACD} \right)\)
Mà \(MN \in \left( {ACD} \right) \Rightarrow BM \bot MN\)