tìm giá trị lớn nhất
A=12x-3x^2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 9 2021
\(C=-3x^2+12x-7=-3\left(x^2-4x+4\right)+12-7=-3\left(x-2\right)^2+5\le5\)
\(maxC=5\Leftrightarrow x=2\)
15 tháng 9 2021
\(C=-3\left(x^2+4x+4\right)+5=-3\left(x+2\right)^2+5\le5\)
Dấu \("="\Leftrightarrow x=-2\)
CM
15 tháng 2 2018
Đáp án C
Có y ' = 6 x 2 + 6 x − 12 ; y ' = 0 ⇔ x = 1 x = − 2 .
Có y − 1 = 15 ; y 1 = − 5 ; y 2 = 6 .
⇒ M a x x ∈ − 1 ; 2 y = 15
CM
24 tháng 12 2018
Đáp án B
Xét hàm số f x = 2 x 3 + 3 x 2 − 12 x + 2 trên đoạn − 1 ; 2 , có f ' x = 6 x 2 + 6 x − 12
Phương trình f ' x = 0 ⇔ − 1 ≤ x ≤ 2 x 2 + x − 2 = 0 ⇔ x = 1
Tính giá trị f − 1 = 15 ; f 1 = − 5 ; f 2 = 6. Vậy m ax − 1 ; 2 f − 1 = 15
CM
23 tháng 9 2018
Đáp án A
Ta có: y ' = 6 x 2 + 6 x − 12 ⇒ y ' = 0 ⇔ x = 1 x = − 2
Suy ra: y − 1 = 15 , y 1 = − 5 , y 2 = 6 ⇒ M = 15 m = − 5 ⇒ M 2 + m 2 = 250.
CM
30 tháng 1 2017
Đáp án D
f x = 2 x 3 - 3 x 2 - 12 x + 10 ⇔ f ' x = 6 x 2 - 6 x - 12 ⇔ x = - 1 ; x = 2
So sánh f - 3 = - 35 , f - 1 = 17 , f 2 = - 10 , f 3 = 1
m a x [ - 3 ; 3 ] f x = 17 ; m i n [ - 3 ; 3 ] f x = - 35 .
CM
3 tháng 10 2018
Chọn đáp án A
Phương pháp
- Tính y’ và tìm nghiệm của y’=0 trên đoạn [-3;3].
- Tính giá trị của hàm số tại hai điểm -3;3 và các điểm là nghiệm của đạo hàm ở trên.
- So sánh kết quả và kết luận.
Cách giải
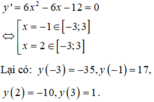
Do đó giá trị lớn nhất của hàm số trên [-3;3] là M=17 và giá trị nhỏ nhất của hàm số trên [-3;3] là m=-35
Vậy T=-18.
=-3x^2+12x-12+12
=-3(x^2-4x+4)+12
==-3(x-2)^2+12<=12
Dấu = xảy ra khi x=2