cho tam giác ABC đều có cạnh là 7
a, tính độ dài đường cao AH
b,từ H kẻ HM⊥AC
tính HM,AM,MC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
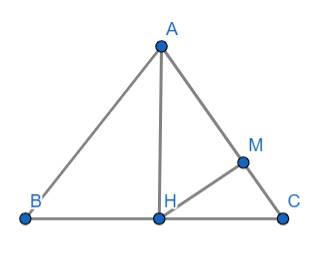
AH là đường cao mà tam giác ABC là tam giác đều nên AH đồng thời là đương trung tuyến
\(\Rightarrow H\) là trung điểm của BC
\(\Rightarrow HB=HC=\dfrac{BC}{2}=\dfrac{7}{2}=3,5\left(cm\right)\)
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow AH=\sqrt{\dfrac{AB^2AC^2}{AB^2+AC^2}}=\sqrt{\dfrac{7^2\cdot7^2}{7^2+7^2}}=\dfrac{7\sqrt{2}}{2}\left(cm\right)\)
Xét tam giác AHC có HM là đường cao ta có:
\(\dfrac{1}{HM^2}=\dfrac{1}{AH^2}+\dfrac{1}{HC^2}\)
\(\Rightarrow HM=\sqrt{\dfrac{AH^2HC^2}{AH^2+HC^2}}=\sqrt{\dfrac{\left(\dfrac{7\sqrt{2}}{2}\right)^2\cdot3,5^2}{\dfrac{7\sqrt{2}}{2}+3,5}}=\dfrac{7\sqrt{6}}{6}\left(cm\right)\)
Xét tam giác AHM vuông tại M áp dụng định lý Py-ta-go ta có:
\(AH^2=HM^2+AM^2\)
\(\Rightarrow AM=\sqrt{AH^2-HM^2}=\sqrt{\left(\dfrac{7\sqrt{2}}{2}\right)^2-\left(\dfrac{7\sqrt{6}}{6}\right)^2}=\dfrac{7\sqrt{3}}{3}\left(cm\right)\)
Mà: \(AM+MC=AC\)
\(\Rightarrow MC=AC-AM=7-\dfrac{7\sqrt{3}}{3}=\dfrac{21-7\sqrt[]{3}}{3}\)
11 tháng 9 2016
BH = 18 cm ; MH = 7 cm ; MC = 25 cm ; AH = 24 cm. Chỉ có đáp án thôi nha!
2 tháng 9 2021
a, Ta có : \(AB=\frac{2}{3}AC\)
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Leftrightarrow\frac{1}{144}=\frac{1}{\left(\frac{2}{3}AC\right)^2}+\frac{1}{AC^2}\Leftrightarrow AC=6\sqrt{13}\)cm
=> \(AB=\frac{2}{3}.6\sqrt{13}=4\sqrt{13}\)cm
Theo định lí Pytago tam giác ABH vuông tại H
\(BH=\sqrt{AB^2-AH^2}=8\)cm
Theo định lí Pytago tam giác AHC vuông tại H
\(CH=\sqrt{AC^2-AH^2}=18\)cm
=> BC = HB + HC = 8 + 18 = 26 cm
b, Vì AM là đường trung tuyến tam giác ABC => BM = MC = BC / 2 = 13 cm
Ta có : BH + MH = BM => MH = BM - BH = 13 - 8 = 5 cm
23 tháng 12 2023
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
b: Xét tứ giác AHKC có
I là trung điểm chung của AK và HC
=>AHKC là hình bình hành
=>AC//KH
c: Ta có: AC//HK
AC//HM
HK,HM có điểm chung là H
Do đó: K,H,M thẳng hàng
Ta có: AMHN là hình chữ nhật
=>\(\widehat{NAH}=\widehat{NMH}\)
mà \(\widehat{NAH}=\widehat{CKH}\)(AHKC là hình bình hành)
nên \(\widehat{NMH}=\widehat{CKH}\)
Xét tứ giác MNCK có CN//MK
nên MNCK là hình thang
Hình thang MNCK có \(\widehat{CKM}=\widehat{NMK}\)
nên MNCK là hình thang cân
d: Ta có: AMHN là hình chữ nhật
=>AH cắt MN tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và MN
Xét ΔCAH có
CO,AI là các đường trung tuyến
CO cắt AI tại D
Do đó: D là trọng tâm của ΔCAH
=>\(AD=\dfrac{2}{3}AI=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AK=\dfrac{1}{3}AK\)
=>AK=3AD
CM
19 tháng 9 2019
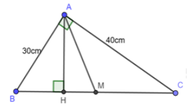
Áp dụng định lý Pytago cho ABH vuông tại A có:
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
Vì AM là đường trung tuyến M là trung điểm BC
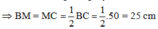
Ta có: MH = BM – BH = 25 – 18 = 7 cm
Đáp án cần chọn là: A
4 tháng 7 2021
đặt AB = x , BC = x + 1 , AC = x + 2 , MH = a
Xét 3 trường hợp
Trường hợp 1 nếu góc B < 90o => BC > AC (khác đề)
Trường hợp 2 nếu góc B = 90 độ (khác đề)
Trường hợp 3 nếu góc B > 90o => AC > BC ( đúng)
Nên ta sẽ đi xét trường hợp 3 : B > 90o ( bạn phải vẽ B > 90o nhé)
HB = MH - BM => HB = a - (x+1)/2 => HB^2 = (a - (x+1)/2)^2
HC = HB + BC => HC = a - x/2 + x => HC^2 = (a + (x+1)/2)^2
Ta có AH^2 = AC^2 - HC^2
AH^2 = AB^2 - HB^2
=> AC^2 - HC^2 = AB^2 - HB^2
<=> (x + 2)^2 - (a+ (x+1)/2)^2 = x^2 - (a - (x+1)/2)^2
<=> x^2 - 4x - 4 - a^2 - ax - a - (x^2+2x+1)/4 = x^2 - a^2 + ax + a - (x^2+2x+1)/4
<=> 2ax + 2a - 4x - 4 = 0
<=> 2a(x+1) - 4(x+1) = 0
<=> (x + 1).2(a - 2) = 0
<=> x = -1 hoặc a = 2
hay AB = -1 hoặc HM = 2 (đpcm)
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=7/2=3,5
\(AH=\sqrt{AB^2-HB^2}=\dfrac{7\sqrt{3}}{2}\)
b: Xét ΔAHC vuông tại H có HM là đường cao
nên HM*AC=AH*HC
=>HM*7=7/2*căn 3*3,5=49/4*căn 3
=>HM=7/4*căn 3
AM=AH^2/AC=21/4
CM=7-21/4=7/4