giúp mình mình giải câu sáu và câu 7 với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
1
AN
26 tháng 5 2021
Gọi x là chiều cao của tam giác ; y là cạnh đáy của tam giác (x,y > 0 )
* chiều cao bằng 3/4 đáy:
x = 3/4y
=> x - 3/4y = 0 (1)
* Nếu chiều cao tăng thêm...tăng thêm 9m^2:
1/2(y-2)(x+3) = 1/2xy + 9 (sau đó bạn tự giải phương trình nha) (2)
Từ (1),(2) suy ra chiều cao là 12m , cạnh đáy là 16m
NK
0
27 tháng 10 2021
Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
27 tháng 10 2021
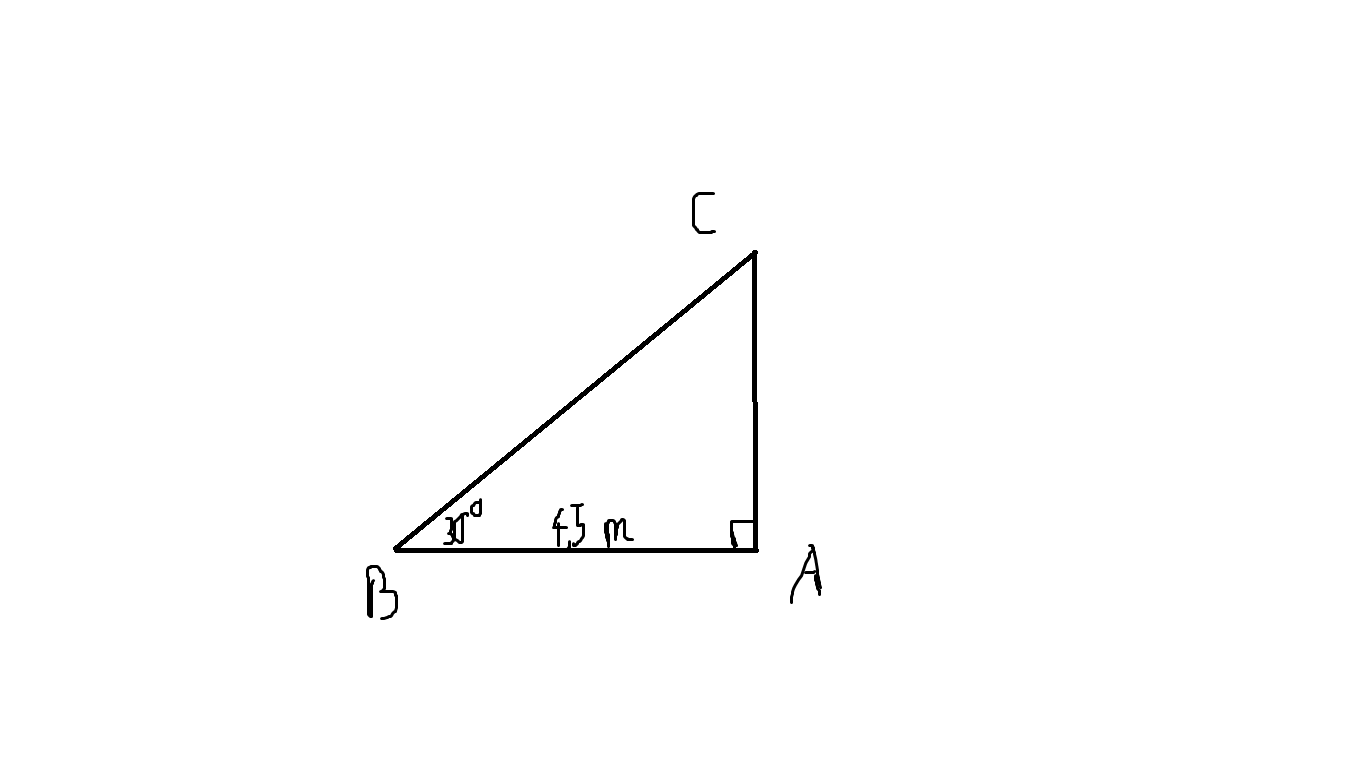
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)
T
1
22 tháng 7 2021
Bài 6:
a) Xét ΔBAC vuông tại A và ΔBAD vuông tại A có
BA chung
AC=AD(gt)
Do đó: ΔBAC=ΔBAD(hai cạnh góc vuông)
Suy ra: \(\widehat{CBA}=\widehat{DBA}\)(hai góc tương ứng)
hay BA là tia phân giác của \(\widehat{DBC}\)
10 tháng 1 2022
Bài 6 :
Vận tốc khi lên đèo :
\(v=\dfrac{s}{t}=\dfrac{45}{2,5}=18\left(\dfrac{km}{h}\right)\)
Vận tốc khi xuống đèo :
\(v=\dfrac{s}{t}=\dfrac{30}{0,5}=60\left(\dfrac{km}{h}\right)\)
Vận tốc tb :
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{45+30}{2,5+0,5}=25\left(\dfrac{km}{h}\right)\)
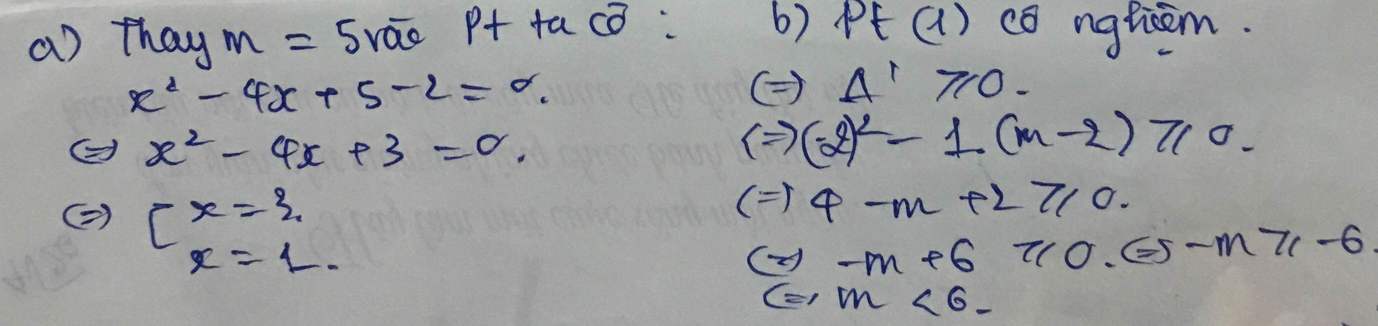
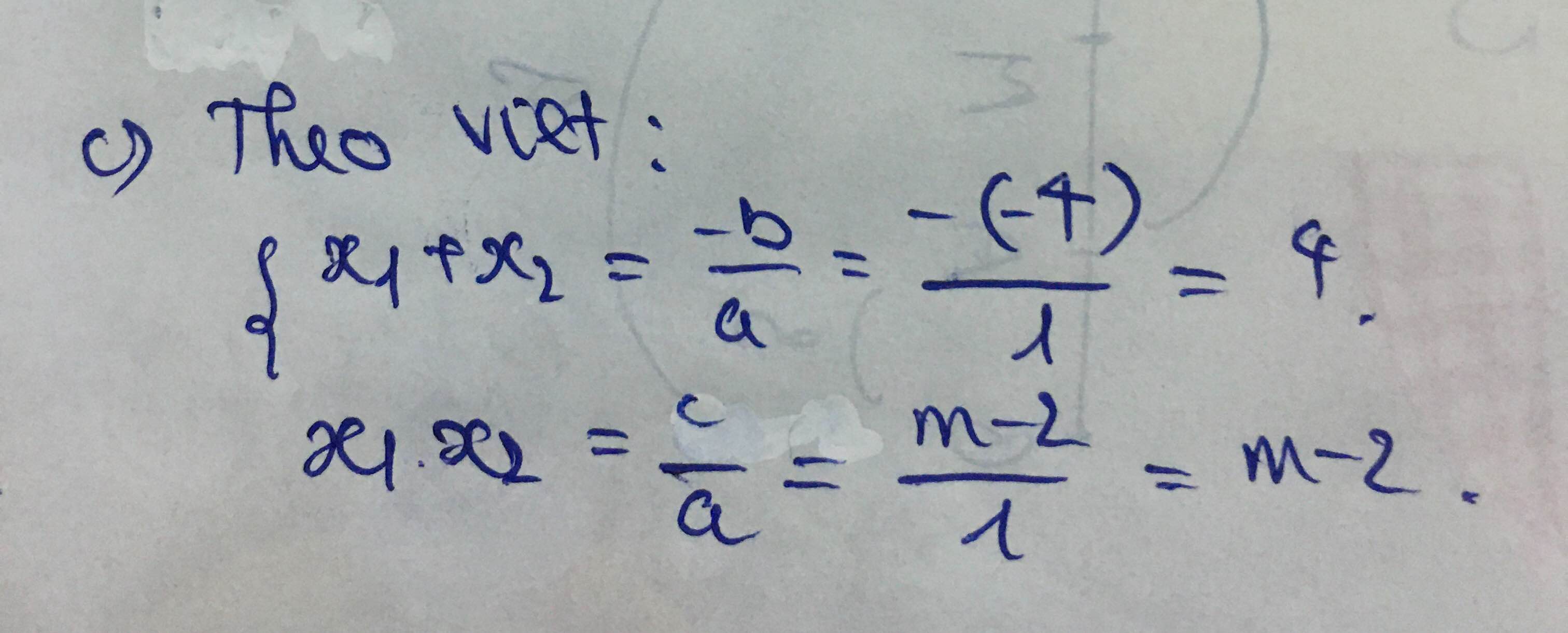
B7:
Diện tích mảnh đất:
30 x 20 = 600(m2)
Bán kính ao:
15:2=7,5(m)
Diện tích ao:
7,5 x 7,5 x 3,14=176,625(m2)
Diện tích phần đất còn lại:
600 - 176,625 = 423,375 (m2)
Đ.số: 423,375m2