Cho Hình Bình Hành ABCD tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt Cd tại F. c/m a...

MQ

Minh Qúy

5 tháng 8 2023

Cho Hình Bình Hành ABCD tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt Cd tại F. c/m a) tam giác ADE = tam giác CBF b) Tứ giác DEBF là HBH c) Tính góc DEB biết góc A = 120...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 8 2023

a: Xét ΔADE và ΔCBF có

góc A=góc C

AD=CB

góc ADE=góc CBF

=>ΔADE=ΔCBF

b: ΔADE=ΔCBF

=>góc AED=góc CFB

=>góc AED=góc FBE

=>DE//BF

Xét tứ giác BEDF có

BE//DF

DE//BF

=>BEDF là hình bình hành

c: góc AED=góc EDC

góc EDC=góc ADE

=>góc AED=góc ADE

=>ΔADE cân tại A

=>góc AED=góc ADE=(180-120)/2=30 độ

góc DEB=180-30=150 độ

Đúng(1)

HK

Hatake Kakashi

24 tháng 8 2017 - olm

Cho hình bình hành ABCD(AB>BC) tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F. Cmr: a) DE//BF

#Toán lớp 8

1

O

OoO_Nhok_Lạnh_Lùng_OoO

24 tháng 8 2017

Cách 1: Tách số hạng thứ hai

x² – 6x + 8 = x² – 2x – 4x + 8

= x(x – 2) – 4( x – 2)

= (x – )(x – 4).

Cách 2: Tách số hạng thứ 3

x² - 6x + 8 = x² – 6x + 9 – 1

= (x – 3)² – 1 = ( x – 3 – 1)(x – 3 + 1)

= (x – 4)( x – 2).

Cách 3: x² – 6x + 8 = x² – 4 – 6x + 12

= ( x – 2)(x + 2) – 6(x – 2)

= (x – 2)(x – 4)

Cách 4: x² – 6x + 8 = x² – 16 – 6x + 24

= ( x – 4)(4 + x) – 6(x – 4)

= (x – 4)( x + 4 – 6)

= (x – 4) ( x – 2).

Cách 5 : x² – 6x + 8 = x² – 4x + 4 – 2x + 4

= (x – 2)² – 2( x – 2)

= (x – 2)( x – 2 – 2)

= ( x – 2)(x – 4).

Đúng(0)

B

Buddy

21 tháng 7 2023

Cho hình bình hành \(ABCD\) (\(AB > BC\)). Tia phân giác của góc \(D\) cắt \(AB\) tại \(E\), tia phân giác của góc \(B\) cắt \(CD\) tại \(F\)

a) Chứng minh \(DE\) // \(BF\)

b) Tứ giác \(DEBF\) là hình gì?

#Toán lớp 8

1

HQ

Hà Quang Minh

Giáo viên

8 tháng 9 2023

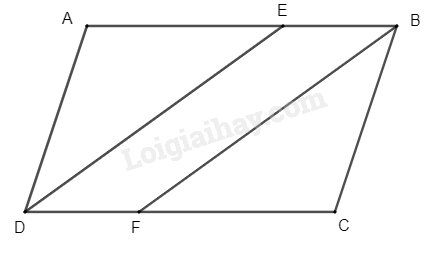
a) Vì \(DE\), \(BF\) là phân giác (gt)

Suy ra \(\widehat {{\rm{ADE}}} = \widehat {{\rm{EDC}}} = \frac{{\widehat {ADC}}}{2}\); \(\widehat {{\rm{EBF}}} = \widehat {{\rm{CBF}}} = \frac{{\widehat {ABC}}}{2}\) (1)

Vì \(ABCD\) là hình bình hành (gt)

Suy ra \(AB\) // \(CD\) và \(\widehat {ADC} = \widehat {ABC}\) (2)

Suy ra \(\widehat {{\rm{AED}}} = \widehat {{\rm{EDC}}}\) (so le trong) (3)

Từ (1), (2), (3) suy ra \(\widehat {AED} = \widehat {ABF}\)

Mà hai góc ở vị trí đồng vị

Suy ra \(DE\) // \(BF\)

b) Xét tứ giác \(DEBF\) ta có:

\(DE\) // \(BF\) (cmt)

\(BE\) // \(DF\) (do \(AB\) // \(CD\))

Suy ra \(DEBF\) là hình bình hành

Đúng(0)

L

Lelemalin

15 tháng 8 2021

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB tại E, tia phân giác của góc B cắt CD tại F. CMR:

a) DE // BF

b) Tứ giác DEBF là hình gì?

c) Tam giác ADE = Tam giác CBF

d) C/m: Tứ giác AECF là hình bình hành

e) AC, DB, EF đồng quy

#Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

15 tháng 8 2021

a: Ta có: \(\widehat{ADE}=\dfrac{\widehat{ADC}}{2}\)

\(\widehat{CBF}=\dfrac{\widehat{CBA}}{2}\)

mà \(\widehat{ADC}=\widehat{CBA}\)

nên \(\widehat{ADE}=\widehat{CBF}\)

Xét ΔADE và ΔCBF có

\(\widehat{ADE}=\widehat{CBF}\)

AD=BC

\(\widehat{DAE}=\widehat{BCF}\)

Do đó: ΔADE=ΔCBF

Suy ra: AE=CF

Ta có: AE+EB=AB

CF+DF=CD

mà AB=CD

và AE=CF

nên EB=DF

Xét tứ giác DEBF có

EB//DF

EB=DF

Do đó: DEBF là hình bình hành

Suy ra: DE//BF

d: Xét tứ giác AECF có

AE//CF

AE=CF

Do đó: AECF là hình bình hành

Đúng(1)

NL

Nguyễn Lê Phước Thịnh

15 tháng 8 2021

e: Ta có: ABCD là hình bình hành

nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường\(\left(1\right)\)

Ta có: EBFD là hình bình hành

nên Hai đường chéo EF và BD cắt nhau tại trung điểm của mỗi đường\(\left(2\right)\)

Từ \(\left(1\right),\left(2\right)\) suy ra AC,BD,EF đồng quy

Đúng(1)

NH

Nguyễn Hải An

4 tháng 7 2023 - olm

Cho hình bình hành ABCD(AB>BC), tia phân giác của góc D cắt AB tại E và tia phân giác của góc B cắt CD tại F.

a) chứng minh 2 tam giác ADE và CBF là những tấm giác cân bằng nhau

b)tứ giác DEBF là hình j, tại sao

#Toán lớp 8

3

LS

Lê Song Phương

4 tháng 7 2023

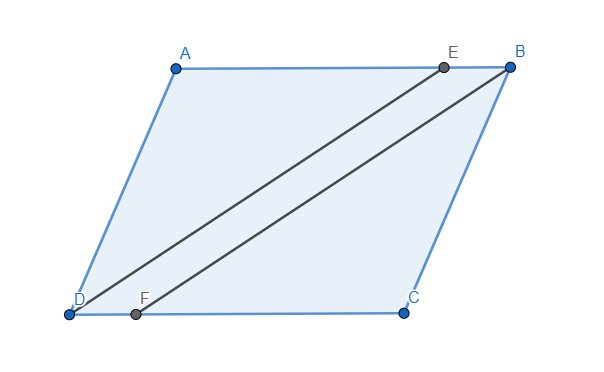
a) Ta thấy \(\widehat{AED}=\widehat{EDC}=\widehat{ADE}\) nên tam giác ADE cân tại A. Hoàn toàn tương tự thì tam giác CBF cân tại C.

Mặt khác, do tứ giác ABCD là hình bình hành nên \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\). Do đó \(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{D}}{2}\) hay \(\widehat{CBF}=\widehat{ADE}\). Kết hợp với \(\widehat{A}=\widehat{C}\) thì suy ra \(\Delta ADE~\Delta CBF\left(g.g\right)\). Lại có \(\dfrac{AD}{CB}=1\) (do tứ giác ABCD là hình bình hành), suy ra \(\Delta ADE=\Delta CBF\) (2 tam giác đồng dạng có tỉ số đồng dạng bằng 1 thì 2 tam giác đó bằng nhau), ta có đpcm.

b) Ta thấy \(\widehat{AED}=\widehat{ADE}=\widehat{CBF}=\widehat{ABF}\) nên DE//BF. Lại có BE//DF (do tứ giác ABCD là hình bình hành) nên tứ giác DEBF cũng là hình bình hành (các cặp cạnh đối song song).

Đúng(1)

NN

Nguyễn Ngọc Anh Minh

CTVHS VIP

4 tháng 7 2023

a/

Xét tg ADE có

\(\widehat{ADE}=\widehat{CDE}\) (gt) (1)

\(\widehat{AED}=\widehat{CDE}\) (góc so le trong) (1)

Từ (1) và (2) => \(\widehat{ADE}=\widehat{AED}\) => tg ADE là tg cân tại A

=> AD=AE (3)

Xét tg CBF có

\(\widehat{CBF}=\widehat{ABF}\) (gt) (4)

\(\widehat{CFB}=\widehat{ABF}\) (góc so le trong) (5)

Từ (4) và (5) => \(\widehat{CBF}=\widehat{CFB}\) => tg CBF cân tại C

=> CB=CF (6)

Ta có

AD=CB (cạnh đối hình bình hành) (7)

Từ (3) (6) (7) => AD=AE=CB=CF

Mà \(\widehat{DAE}=\widehat{BCF}\) (góc đối hình bình hành)

=> tg ADE = tg CBF (c.g.c)

=> tg ADE và tg CBF là những tg cân bằng nhau

b/

tg ADE = tg CBF (cmt) \(\Rightarrow\widehat{BFC}=\widehat{ADE}\)

Mà \(\widehat{EDC}=\widehat{ADE}\) (gt)

\(\Rightarrow\widehat{BFC}=\widehat{EDC}\) Hai góc này ở vị trí đồng vị => DE//BF (8)

Ta có

AB//CD (cạnh đối hình bình hành) => BE//DF (9)

Từ (8) (9) => DEBF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hình bình hành)

Đúng(1)

NA

Nguyễn Anna

24 tháng 10 2016 - olm

Cho hình bình hành ABCD, tia phân giác của góc D và góc B cắt AB và CD tại M và N

a, CHứng minh DM// BN

b, CHứng minh DMBN là hình bình hành

c, Tia phân giác của góc A cắt DM và BN tại H và G

Tia phân giác của góc C cắt DM và BN tại E và F
CHứng minh HEFG là hình chư nhật

#Toán lớp 8

1

VL

Vil Love Zoi

24 tháng 10 2016

Bạn tự vẽ hình nhá!!!!

a) ABCD là hình bình hành=>góc ADC=góc ABC => góc MBN=góc MDN

Mà: góc MBN= góc BNC( so le trong) => góc BNC=góc MDN => DM//BN

b) Từ phần a ta có:

Xét DMNB có DM//BN

BM//DN (do AB//CD)

=> DMNB là hbh

c) Ta có:

góc AMD= góc MDC(so le trong) => góc ADM= góc AMD=> Tam giác AMD cân tại A

Mà: AH là đường phân giác=> AH là đường cao<=> AH vuông góc với DM (1)

=>AG vuông góc với BN ( do DM//BN) (2)

Tương tự, ta cũng chứng minh được tam giác BNC cân tại C

Mà: CF là đường PG=> CF vuông góc với BN (3)

Từ (1); (2); (3) => HEFG là hcn do có 3 góc vuông

Đúng(0)

PX

Phạm Xuân Bách

26 tháng 10 2020 - olm

Câu hỏi hay

cho hình bình hành abcd (ab>cd) tia phân giác góc a cắt CD tại I tia phân giác góc c cắt ab tại K .Phân giác góc D cắt AI,CKthuws tự tại H,E.Phân giác gó B cắt AI,CK theo thứ tự tại G,F CMR GE=HF

#Toán lớp 8

0

NL

Nguyễn Lan Hương

16 tháng 10 2020 - olm

Cho hình bình hành ABCD ( AB> BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a. c/m DE // BF

b. tứ giác DEBF là hình j

#Toán lớp 8

0

KM

Khánh Mai

9 tháng 11 2021

cho hình bình hành ABCD (AB>BC).Tia phân giác của góc D cắt AB ở E,tia phân giác của góc B cắt CD ở F chứng minh DE=BF

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

9 tháng 11 2021

Xét ΔADE và ΔCBF có

\(\widehat{ADE}=\widehat{CBF}\)

AD=CB

\(\widehat{A}=\widehat{C}\)

Do đó: ΔADE=ΔCBF

Suy ra: DE=BF

Đúng(0)

PT

Pham Trong Bach

2 tháng 11 2018

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh DE//BE.

b) Tứ giác DEBF là hình gì?

#Toán lớp 8

1

CM

Cao Minh Tâm

2 tháng 11 2018

a) Ta có A E D ^ = E D C ^ v à A B F ^ = E D C ^ ⇒ D E / / B F (có góc ở vị trí đồng vị bằng nhau).

b) Từ câu a) suy ra DEBF là hình bình hành.

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP