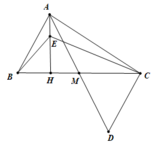
cho tam giác ABC có AC>AB, trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD=MA, nối C với D
a) CM \(\widehat{DAC}\)< \(\widehat{ADC}\).Từ đố suy ra \(\widehat{MAB}\)>\(\widehat{MAC}\)
b) Kẻ đường cao Ah, gọi E là một điểm nằm giữa A và H. So sánh HC và HB; EC và EB

a) Xét \(\Delta\)BAM và \(\Delta\)CDM có:
MB=MC
^AMB=^DMC => \(\Delta\)BAM=\(\Delta\)CDM (c.g.c)
MA=MD
=> AB=DC (2 cạnh tương ứng). Mà AB<AC =>DC<AC => ^DAC<^ADC (Qhệ góc và cạnh đối diện)
^ADC=^BAM (2 góc tương ứng) => ^BAM>^CAM hay ^MAB>^MAC (đpcm)
b) AH \(⊥\)BC , AC>AB => HC>HB (Qhệ đường xiên hình chiếu)
E nằm giữa A và H => EH\(⊥\)BC, HC>HB => EC>EB.