Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
=>ΔAHD=ΔBKC
b: Xét tứ giác ABKH có
AB//KH
AH//BK
=>ABKH là hình bình hành
=>AB=KH
a, Ta có : \(DC=2AB=2.6=12\left(cm\right)\)
\(\Rightarrow S_{ABCD}=\dfrac{\left(AB+CD\right).AH}{2}=\dfrac{\left(6+12\right).4}{2}=36\left(cm^2\right)\)
b, Xét ΔAHD và ΔBKC có :
\(\widehat{AHD}=\widehat{BKC}=90^0\)
\(\widehat{D}=\widehat{C}\left(ABCD\cdot là\cdot hình\cdot thang\cdot cân\right)\)
\(\Rightarrow\Delta AHD\sim\Delta BKC\left(g-g\right)\)
c, Ta có : \(\Delta AHD\sim\Delta BKC\left(cmt\right)\)
\(\Rightarrow\dfrac{AH}{BK}=\dfrac{AD}{BC}\)
\(\Rightarrow AH.BC=AD.BK\left(đpcm\right)\)
a: DC=6*2=12cm
S ABCD=1/2(AB+CD)*AH
=1/2*4*(6+12)=2*18=36cm2
b: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
góc D=góc C
=>ΔAHD đồng dạng với ΔBKC
c: ΔAHD đồng dạng với ΔBKC
=>AD/BC=AH/BK
=>AH*BC=AD*BK
a: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
góc D=góc C
=>ΔAHD=ΔBKC
Xét tam giác ADH và tam giác BCK có:
góc AHD= góc BKC
DA= BC (ABCD là hình thang cân)
góc D = góc C (ABCD là htc)
=> tam giác ADH = tam giác BCK (ch-gn)
=> HD = KC (đpcm)
Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
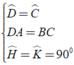
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)
