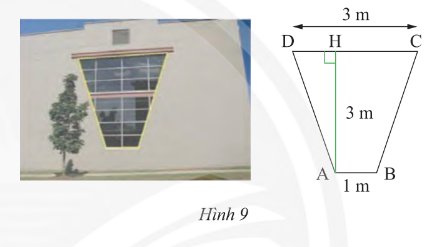
Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
28 tháng 1 2022
a) P= (18+8).2=52 (cm) ; S=18.8=144 (cm2)
b) P=6.4=24 (cm) ; S= 62=36 (cm2)
c) P=4+10+5+5=24 (cm) ; S= \(\dfrac{\left(4+10\right).4}{2}\)=28 (cm2)
d) P=5.4=20 (cm) ; S= \(\dfrac{6.8}{2}\)=24 (cm2)
e) P=(10+14).2=48 (cm2) ; S (chiều cao ứng với cạnh 10cm)=10.8=80cm2; S (chiều cao ứng với cạnh 14cm)=14.8=112cm2
29 tháng 7 2023
Chiều dài khung hình chữ nhật là (7+1)/2=4m
Chiều rộng khung hình chữ nhật là 4-1=3m
Nếu cạnh đáy là chiều rộng của hình chữ nhật thì chiều cao sẽ là 3-3=0(loại)
=>Cạnh đáy sẽ là chiều dài của hình chữ nhật
Chiều cao ứng với cạnh đáy là 4-3=1m
Diện tích khung hìnhbình hành là:
1*4=4m2
HQ
Hà Quang Minh
Giáo viên
10 tháng 10 2023
a) \(a = 20cm;h = 5cm\).
Áp dụng công thức tính diện tích ta có:
\(S =20.5=100 \left( {c{m^2}} \right)\).
b) \(m = 5\left( m \right);n = 20\left( {dm} \right) = 2\left( m \right)\)
\( \Rightarrow S = \frac{{m.n}}{2} = \frac{{5.2}}{2} = 5\left( {{m^2}} \right)\)
c) \(a = 5\left( m \right);b = 3,2\left( m \right);h = 4\left( m \right)\)
\( \Rightarrow S = \frac{{\left( {a + b} \right).h}}{2} = \frac{{\left( {5 + 3,2} \right).4}}{2} = 16,4\left( {{m^2}} \right)\).
TA
19 tháng 7 2023
a) Thể tích phòng: 5.4.3=60 (m khối)
b)Diện tích xung quanh căn phòng là:
2.(5+4).3= 54(m vuông)
Diện tích cửa là: 1.2 = 2 (m vuông)
Diện tích cửa sổ là: 1.1,5=1,5 (m vuông)
Diện tích cần sơn là: 54 - 2 - 1,5 = 50,5 (m vuông)
c)Diện tích 1 cuộn là:
10.0,53=5,3 (m vuông)
Cần đặt số cuộn giấy là:
50,5/5,3 xấp xỉ bằng 9,5 nhưng để dự phòng thì cần ít nhất 10 cuộn bn nhé:)
18 tháng 12 2021
\(a,S=15.6=90\left(cm^2\right)\\ b,S=\dfrac{1}{2}\cdot4\cdot250=500\left(cm^2\right)\\ c,S=\dfrac{1}{2}\left(7+4\right)\cdot3,5=19,25\left(m^2\right)\)
KV
7 tháng 12 2023
a) Diện tích hình bình hành:
\(15.6=90\left(cm^2\right)\)
b) 25 dm = 250 cm
Diện tích hình thoi:
\(4\times250:2=500\left(cm^2\right)\)
c) Diện tích hình thang cân:
\(\left(7+4\right)\times3,5:2=19,25\left(m^2\right)\)
19 tháng 10 2021
TL:
a) Diện tích hình vuông là:
5 x 5 = 25 ( cm2 )
Đ/S: 25cm2
Kẻ đường cao \(BK\)
Suy ra \(AH = BK\) và \(AHKB\) là hình chữ nhật
Suy ra \(HK = AB = 1\)cm
Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AD = BC\) (tc)
Xét \(\Delta AHD\) và \(\Delta BKC\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{BKC}}} = 90^\circ \) (gt)
\(\widehat D = \widehat C\) (định nghĩa hình thang cân)
\(AD = BC\) (tính chất hình thang cân)
Suy ra: \(\Delta AHD = \Delta BKC\) (ch – cgv)
Suy ra \(DH = KC\) (hai cạnh tương ứng)
Suy ra \(DH = KC = \frac{{CD - HK}}{2} = \frac{{3 - 1}}{2} = 1\) (cm)
Suy ra \(HC = 2\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(AHD\) ta có:
\(A{D^2} = D{H^2} + A{H^2} = {1^2} + {3^2} = 10\)
Suy ra \(AD = \sqrt {10} \) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(ACH\) ta có:
\(A{C^2} = A{H^2} + H{C^2} = {3^2} + {2^2} = 9 + 4 = 13\)
\(AC = \sqrt {13} \) (cm)
Vậy \(AC = BD = \sqrt {13} \)cm; \(AD = BC = \sqrt {10} \) cm