Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình thang ABCD có các đường cao AH và BK. Từ A kẻ đường thẳng song song với BD cắt CD ở E Þ AB = ED.
Chứng minh A C H ^ = 45 0 . Do DEAC vuông cân ở A nên A H = C H = E H = A B + C D 2

Câu 11:
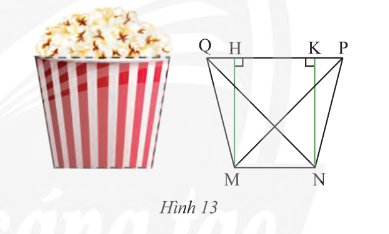
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB

1/
Kẻ AH \(\perp\)CD , \(BK\perp CD\)
Xét tam giác vuông AHD và tam giác vuông BKC, có: góc ADH = góc BCK = 600 ; cạnh AH = BK
=> tam giác AHD = tam giác BKC (gcg)
=> DH = KC
Đặt a = DH (a > 0) => AH = \(\sqrt{1-x^2}\)
Có: Sin60 = \(\frac{AH}{AD}\Rightarrow\frac{\sqrt{3}}{2}=\sqrt{1-x^2}\Rightarrow1-x^2=\frac{3}{4}\Rightarrow x^2=\frac{1}{4}\Rightarrow\left[\begin{array}{nghiempt}x=\frac{1}{2}\left(n\right)\\x=-\frac{1}{2}\left(l\right)\end{array}\right.\)
=> x = 1/2 hay DH = KC = 1/2
Mặt khác: HK = CD - (DH + KC) = 2,7 - (1/2 + 1/2) = 1,7 (m)
Tứ giác ABCD là hình chữ nhật (góc AHK = góc BKH = ABK = 900) => AB = HK = 1,7 (m)
Vậy AB = 1,7m
2/
a/ Cm: tam giác ICD đều:
Trong tam giác ICD : DB vừa là đường phân giác , vừa là đường cao => tam giác ICD là tam giác cân tại D
=> ID = DC (1)
=> DB vừa là đường trung tuyến => BI = BC = 4cm => IC = 4 + 4 = 8cm (2)
Có: góc IAB = IDC (đồng vị) , góc IBA = góc ICD (đồng vị)
mà góc IDC = góc ICD
=> góc IAB = góc IBA => tam giác IAB cân tại I => IA = IB = 4cm
=> ID = IA + AD = 4 + 4 = 8cm (3)
Từ (1), (2), (3) => ID = DC = IC = 8cm hay tam giác IDC đều
b/ Tính chu vi hình thang ABCD:
Vì tam giác ICD đều => tam giác IAB đều => IA = AB = 4cm
ID = DC = 8cm
Vậy chu vi hình thang ABCD : AB + AD + BC + CD = 4 + 4 + 4 + 8 = 20(cm)
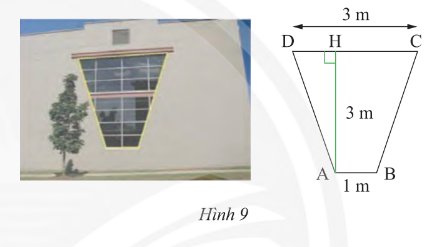


Kẻ đường cao \(BK\)
Suy ra \(AH = BK\) và \(AHKB\) là hình chữ nhật
Suy ra \(HK = AB = 1\)cm
Vì \(ABCD\) là hình thang cân (gt)
\( \Rightarrow AC = BD\) và \(AD = BC\) (tc)
Xét \(\Delta AHD\) và \(\Delta BKC\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{BKC}}} = 90^\circ \) (gt)
\(\widehat D = \widehat C\) (định nghĩa hình thang cân)
\(AD = BC\) (tính chất hình thang cân)
Suy ra: \(\Delta AHD = \Delta BKC\) (ch – cgv)
Suy ra \(DH = KC\) (hai cạnh tương ứng)
Suy ra \(DH = KC = \frac{{CD - HK}}{2} = \frac{{3 - 1}}{2} = 1\) (cm)
Suy ra \(HC = 2\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(AHD\) ta có:
\(A{D^2} = D{H^2} + A{H^2} = {1^2} + {3^2} = 10\)
Suy ra \(AD = \sqrt {10} \) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(ACH\) ta có:
\(A{C^2} = A{H^2} + H{C^2} = {3^2} + {2^2} = 9 + 4 = 13\)
\(AC = \sqrt {13} \) (cm)
Vậy \(AC = BD = \sqrt {13} \)cm; \(AD = BC = \sqrt {10} \) cm