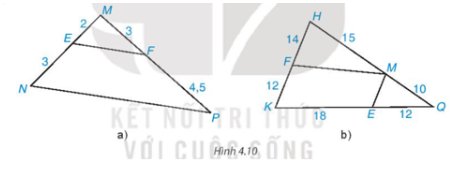
Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 3 2019
a) Xét hình 13a) : MN // AB.
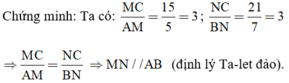
⇒ MN // AB (Theo định lý Ta-let đảo).
b) Xét hình 13b) : AB // A’B’ // A”B”.
Ta có: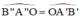 
⇒ A’B’ // A”B” (Hai góc so le trong bằng nhau).
Lại có:
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
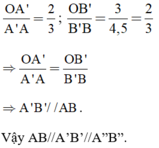
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.
22 tháng 4 2017
Trên hình 13a ta có:
APPBAPPB = 3838; AMMCAMMC= 515515 = 1313 vì 3838 ≠ 1313 nên APPBAPPB ≠ AMMCAMMC => PM và MC không song song.
Ta có CNNB=217=3CMMA=155=3}=>CMMA=CNNBCNNB=217=3CMMA=155=3}=>CMMA=CNNB => MN//AB
Trong hình 13b
Ta có: OA′A′AOA′A′A = 2323; OB′B′BOB′B′B = 34,534,5 = 2323
=>
KV
19 tháng 10 2023
*) Hình 8
Ta có:
∠C + ∠MNC = 65⁰ + 115⁰
= 180⁰
Mà ∠C và ∠MNC là hai góc trong cùng phía
⇒ MN // BC
*) Hình 9
Ta có:
∠C + ∠NMC = 30⁰ + 150⁰
= 180⁰
Mà ∠C và ∠NMC là hai góc trong cùng phía
⇒ MN // BC
*) Hình 10
Ta có:
∠ANx + ∠ANM = 180⁰ (kề bù)
⇒ ∠ANM = 180⁰ - ∠ANx
= 180⁰ - 110⁰
= 70⁰
⇒ ∠ANM = ∠NBC = 70⁰
Mà ∠ANM và ∠NBC là hai góc đồng vị
⇒ MN // BC
*) Hình 11
Ta có:
∠x'Az + ∠x'AB = 180⁰ (kề bù)
⇒ ∠x'AB = 180⁰ - ∠x'Az
= 110⁰ - 130⁰
= 50⁰
⇒ ∠x'AB = ∠y'Bz' = 50⁰
Mà ∠x'AB và ∠x'Az' là hai góc đồng vị
⇒ xx' // yy'
H9
HT.Phong (9A5)
CTVHS
19 tháng 10 2023
Bài 8:
Ta có: \(a//b\Rightarrow\widehat{D_1}=\widehat{DAB}\) (đồng vị)
Mà: \(\widehat{DAB}=90^o\)
\(\Rightarrow\widehat{D_1}=90^o\)
Và: \(a//b\Rightarrow\widehat{DCB}=\widehat{B_1}\) (so le trong)
Mà: \(\widehat{DCB}=130^o\)
\(\Rightarrow\widehat{B_1}=130^o\)
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Xét hình a: a // b vì đường thẳng c cắt 2 đường thẳng a, b và tạo thành một cặp góc so le trong bằng nhau
Xét hình b: không có cặp đường thẳng nào song song vì đường thẳng g cắt 2 đường thẳng d, e và không tạo thành một cặp góc so le trong bằng nhau ( 90 \(^\circ \) 80 \(^\circ \))
Xét hình c: m // n vì đường thẳng p cắt 2 đường thẳng m, n và tạo thành một cặp góc đồng vị bằng nhau
g mỗi trường hợp hình vẽ có hai đường thẳng song song với nhau. Tìm ra và kể tên hai đường thẳng song song với nhau đó. Giải thích các hiểu của em.
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Vì \(\widehat {{A_1}} = \widehat {{B_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên z // t
b) Vì \(\widehat {{D_1}}= \widehat {{C_1}} (= 90^\circ) \)
Mà 2 góc này ở vị trí đồng vị nên m // n
c) Vì \(\widehat {{E_1}} + \widehat {{E_2}} = 180^\circ \) ( 2 góc kề bù) nên \(110^\circ + \widehat {{E_2}} = 180^\circ \Rightarrow \widehat {{E_2}} = 180^\circ - 110^\circ = 70^\circ \)
Vì \(\widehat {{E_2}} = \widehat {{G_1}}( = 70^\circ )\). Mà 2 góc này ở vị trí so le trong nên x // y
d) Vì \(\widehat {{K_1}} + \widehat {{K_2}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{K_1}} + 56^\circ = 180^\circ \Rightarrow \widehat {{K_1}} = 180^\circ - 56^\circ = 124^\circ \)
Vì \(\widehat {{H_1}} = \widehat {{K_1}}( = 124^\circ )\). Mà 2 góc này ở vị trí so le trong nên u // v
CM
2 tháng 12 2017
a)
b) Các cặp cạnh song song với nhau có trong hình tứ giác ADCB là: cặp cạnh AD và BC, AB và DC.
24 tháng 7 2023
`a, AB` không song song `CD`
`b, EG` song song `HI`
`c, MN` không song song `PQ`
`d, ST` song song `XY`
• Hình 4.10a)
Ta có: \(\dfrac{{EM}}{{EN}} = \dfrac{2}{3};\dfrac{{MF}}{{PF}} = \dfrac{3}{{4,5}} = \dfrac{2}{3}\) nên \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\)
Vì \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\), E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.
• Hình 4.10b)
* Ta có: \(\dfrac{{HF}}{{KF}} = \dfrac{{14}}{{12}} = \dfrac{7}{6};\dfrac{{HM}}{{MQ}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\)
Vì \(\dfrac{{HF}}{{KF}} \ne \dfrac{{HM}}{{MQ}}\) nên MF không song song với KQ.
* Ta có: \(\dfrac{{MQ}}{{MH}} = \dfrac{{10}}{{15}} = \dfrac{2}{3};\dfrac{{EQ}}{{EK}} = \dfrac{{12}}{{18}} = \dfrac{2}{3}\)
Vì \(\dfrac{{MQ}}{{MH}} = \dfrac{{EQ}}{{EK}}\); F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.