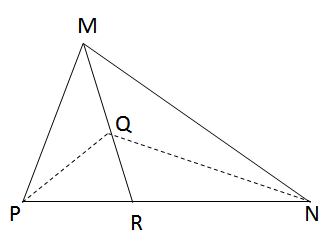
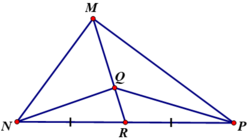
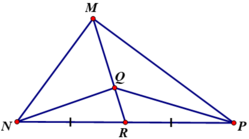
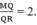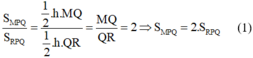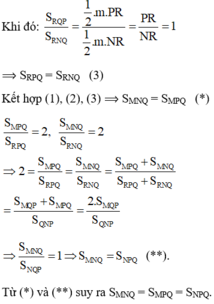cho tam giác MNP và đường trung tuyến MRvaof trọng tâm Q
a) Tính tỉ số các diện tích của hai tam giác MPQ và RPQ
b)tỉ số các diện tích của hai tam giác MNQ và RNQ
c) so sánh các diện tích chủa hai tam giacsRPQ và RNQ
Từ các kết quả trên, hãy chứng minh các tam giác QMN,QNP,QPM có cùng diện tích
ai lm đúng mình tích cho