Hãy vận dụng công thức \(V=\dfrac{A}{q}\) để chứng tỏ rằng công thực hiện để dịch chuyển điện tích q từ điểm N đến điểm M bằng: AMN = (VM - VN)q = UMNq
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công thức 19.2:
\(W_M=A_{M\infty}\)
Công thức 19.3:
\(W_M=V_Mq\)
Điện thế tại điểm M:
\(V_M=\dfrac{W_M}{q}=\dfrac{A_{M\infty}}{q}\) và \(V=\dfrac{A}{q}\)

Đáp án B
+ Mối liên hệ giữa công và hiệu thế năng A M N = q . V M - V N

Tham khảo:
Chúng ta đã biết rằng, công của lực điện trong sự dịch chuyển điện tích q không phụ thuộc vào hình dạng quãng đường mà chỉ phụ thuộc vào vị trí điểm đầu và điểm cuối của độ dịch chuyển. Do đó, nếu xét dịch chuyển từ điểm M đến vô cực theo hai cung đường khác nhau từ M đến vô cùng mà cung đường thứ hai đi qua điểm N ta sẽ có cùng kết quả:
AM∞ = AMN∞=WM (1)
Mặt khác: AM∞ = AMN + AN∞ =AMN + WN (2)
Từ (1) và (2) ta có:
WM = AMN +WN hay bằng AMN = WM - WN

Chọn đáp án A.
Công của lực điện khi di chuyển điện tích q giữa hai điểm M, V là A = q U M N

Chọn đáp án A.
Công của lực điện khi dịch chuyển điện tích q giữa hai điểm M, V là A = qUMN.
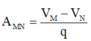

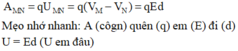
Hiệu điện thế UMN bằng độ biến thiên thế năng từ M đến N: UMN = VM - VN
\({V_{MN}} = \frac{{{A_{MN}}}}{q}\) ⇒ ANM = (VM−VN)q = UMN.q