Hãy chứng minh rằng độ lệch pha giữa hai dao động cùng chu kì bằng độ lệch pha ban đầu.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
27 tháng 8 2023
Giả sử hai dao động có phương trình tổng quát là:
\(\left\{{}\begin{matrix}x_1=A_1cos\left(\omega t+\varphi_1\right)\\x_2=A_2cos\left(\omega t+\varphi_2\right)\end{matrix}\right.\)
Độ lệch pha giữa hai dao động là: \(\Delta\varphi=\left(\omega t+\varphi_2\right)-\left(\omega t+\varphi_1\right)=\varphi_2-\varphi_1\)
HQ
Hà Quang Minh
Giáo viên
27 tháng 8 2023
Độ lệch pha là đại lượng đặc trưng cho độ lệch về thời gian giữa hai dao động điều hoà cùng chu kì.
Chọn D.
VT
2 tháng 12 2018
Đáp án B
Độ lệch pha giữa hai dao động vẫn không thay đổi theo thời gian
VT
7 tháng 11 2019
Đáp án B
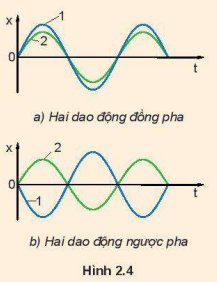
+ Độ lệch pha giữa hai dao động ngược pha → Δ φ = π .
VT
8 tháng 9 2017
Chọn đáp án C
+ Hai dao động được gọi là ngược pha nếu Δφ = π
HQ
Hà Quang Minh
Giáo viên
27 tháng 8 2023
Hai dao động có cùng biên độ.
Ở cùng một thời điểm khi dao động 1 ở vị trí cân bằng thì dao động 2 ở vị trí bên và ngược lại.
VT
23 tháng 10 2017
Đáp án A.
Ta có:
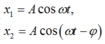
– Hai chất điểm có cùng li độ:
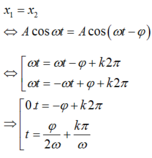
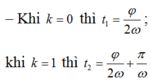
– Khoảng thời gian ngắn nhất giữa hai lần các chất điểm có cùng li độ là:
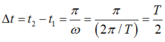
Độ lệch pha của hai dao động ở thời điểm t bất kì là: \(\Delta\phi=\left(\omega_2t+\varphi_2\right)-\left(\omega_1t+\varphi_1\right)\)
Vì 2 dao động có cùng chu kì nên \(\omega_1=\omega_2\)
Vậy \(\Delta\phi=\varphi_2-\varphi_1\)