Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a√3 . O là tâm hình vuông . Chứng minh (SAC) vuông góc (ABCD) ; (SAC) vuông góc (SBD)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
a: SO vuông góc (ABCD)
=>(SAC) vuông góc (ABCD)
b: AC vuông góc BD
BD vuông góc SO
=>BD vuông góc (SAC)
=>(SBD) vuông goc (SAC)
6 tháng 7 2023
a: AC vuông góc BD
AC vuông góc SO
=>AC vuông góc (SBD)
=>SB vuông góc AC
mà AC vuông góc BD
nên AC vuông góc (SBD)
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=>BD vuông góc SA
b: Xét ΔACB có CO/CA=CI/CB
nên OI//AB
=>OI vuông góc BC
BC vuông góc OI
BC vuông góc SO
=>BC vuông góc (SOI)
=>(SBC) vuông góc (SOI)
CM
9 tháng 6 2019
a) Theo giả thiết, S.ABCD là hình chóp đều và đáy ABCD là hình vuông nên SO ⊥ (ABCD) ( tính chất hình chóp đều)
Đáy ABCD là hình vuông cạnh a nên
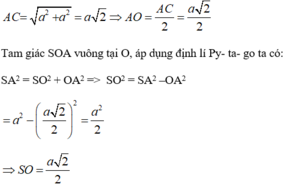
=> Góc giữa hai mặt phẳng (MBD) và (ABCD) là 45 o
CM
26 tháng 10 2017
Đáp án D
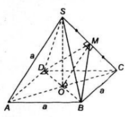
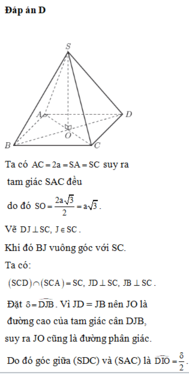
Ta có A C = 2 a = S A = S C suy ra tam giác SAC đều, do đó S O = 2 a 3 2 = a 3 . Vẽ D J ⊥ S C , J ∈ S C . Khi đó BJ vuông góc với SC.
Ta có: S C D ∩ S C A = S C , J D ⊥ S C , J B ⊥ S C . Đặt δ = D J B ^ . Vì JD = JB nên JO là đường cao của tam giác cân DJB, suy ra JO cũng là đường phân giác. Do đó góc giữa (SDC) và (SAC) là D I O ^ = δ 2 .
Ta có S C ⊥ D J B , mà O J ⊂ D J B nên O J ⊥ S C . Trong Δ D J O ta có: O J = O D . cot δ 2 . Trong Δ S O C ta có: 1 O J 2 = 1 O S 2 + 1 O A 2 ⇔ 1 a 2 cot 2 δ 2 = 1 3 a 2 + 1 a 2
Do đó: 1 a 2 cot 2 δ 2 = 4 3 a 2 ⇔ cot 2 δ 2 = 3 4 ⇔ 1 + cot 2 δ 2 = 7 4
⇔ 1 sin 2 δ 2 = 7 4 ⇔ sin 2 δ 2 = 4 7 ⇔ cos 2 δ 2 = 3 7
Mà cos δ 2 > 0 nên từ (1) ta có cos δ 2 = 21 7 . Vậy côsin của góc giữa (SDC) và ( S A C ) bằng 21 7
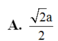
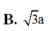
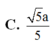
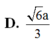
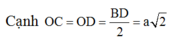
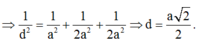
Mai thi ạ giúp gấp với
Do S.ABCD là chóp tứ giác đều \(\Rightarrow SO\perp\left(ABCD\right)\)
Mà \(O\in AC\Rightarrow SO\in\left(SAC\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
Ta có: \(\left\{{}\begin{matrix}SO\perp\left(ABCD\right)\Rightarrow SO\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(BD\in\left(SBD\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)