Giúp mình câu 7,9, mình cảm ơn.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
1
26 tháng 8 2021
Câu 10:
a) \(B=\left(\dfrac{\sqrt{a}-2}{\sqrt{a}+2}+\dfrac{\sqrt{a}+2}{\sqrt{a}-2}-\dfrac{4a}{4-a}\right):\dfrac{3a+4}{\sqrt{a}+2}\)
\(=\dfrac{\left(\sqrt{a}-2\right)^2+\left(\sqrt{a}+2\right)^2+4a}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}.\dfrac{\sqrt{a}+2}{3a+4}=\dfrac{a-4\sqrt{a}+4+a+4\sqrt{a}+4+4a}{\left(\sqrt{a}-2\right)\left(3a+4\right)}=\dfrac{6a+8}{\left(\sqrt{a}-2\right)\left(3a+4\right)}=\dfrac{2\left(3a+4\right)}{\left(\sqrt{a}-2\right)\left(3a+4\right)}=\dfrac{2}{\sqrt{a}-2}\)
b)Ta có: \(\sqrt{a}-2\ge-2\Rightarrow\dfrac{2}{\sqrt{a}-2}\le-1\)
Để \(B< -1\) thì \(\dfrac{2}{\sqrt{a}-2}\ne-1\Leftrightarrow\sqrt{a}-2\ne-2\Leftrightarrow a\ne0\) và \(a\ge0,a\ne4\)
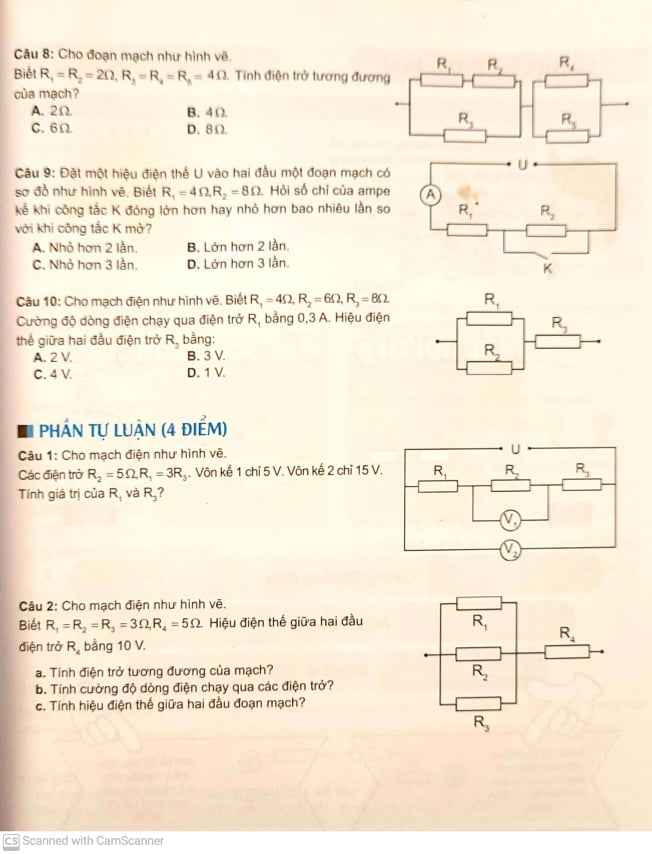
Câu 11:
a) \(P=\left(\dfrac{\sqrt{x}-4x}{1-4x}-1\right):\left(\dfrac{1+2x}{1-4x}-\dfrac{2\sqrt{x}}{1-2\sqrt{x}}-1\right)=\dfrac{\sqrt{x}-4x-1+4x}{1-4x}:\dfrac{1+2x-2\sqrt{x}\left(1+2\sqrt{x}\right)-1+4x}{1-4x}=\dfrac{\sqrt{x}-1}{1-4x}.\dfrac{1-4x}{2x-2\sqrt{x}}=\dfrac{\sqrt{x}-1}{2\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{1}{2\sqrt{x}}\)
b) Thay x=\(3-2\sqrt{2}\) vào P ta được:
\(P=\dfrac{1}{2\sqrt{x}}=\dfrac{1}{2\sqrt{3-2\sqrt{2}}}=\dfrac{1}{2\left(\sqrt{\sqrt{2}-1}\right)^2}=\dfrac{1}{2\left(\sqrt{2}-1\right)}=\dfrac{1+\sqrt{2}}{2}\)
c) \(P=\dfrac{1}{2\sqrt{x}}>\dfrac{1}{2}\Leftrightarrow2\sqrt{x}< 2\Rightarrow0< x< 1\) và \(x\ne\dfrac{1}{4}\)
LT
1
N
1
HP
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2021
d. \(\dfrac{\pi}{2}< a;b< \pi\Rightarrow sina>0;sinb>0\)
\(sina=\sqrt{1-cos^2a}=\dfrac{4}{5}\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{4}{3}\)
\(sinb=\sqrt{1-cos^2b}=\dfrac{5}{13}\Rightarrow tanb=-\dfrac{5}{12}\)
Vậy:
\(sin\left(a-b\right)=sina.cosb-cosa.sinb=\dfrac{4}{5}.\left(-\dfrac{12}{13}\right)-\left(-\dfrac{3}{5}\right)\left(\dfrac{5}{13}\right)=...\)
\(cos\left(a-b\right)=cosa.cosb-sina.sinb=...\) (bạn tự thay số bấm máy)
\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}=...\)
\(cot\left(a+b\right)=\dfrac{1}{tan\left(a+b\right)}=\dfrac{1-tana.tanb}{tana+tanb}=...\)
e.
\(0< y< \dfrac{\pi}{2}\Rightarrow cosy>0\Rightarrow cosy=\sqrt{1-sin^2y}=\dfrac{4}{5}\)
\(\Rightarrow tany=\dfrac{siny}{cosy}=\dfrac{3}{4}\)
Vậy: \(tan\left(x+y\right)=\dfrac{tanx+tany}{1-tanx.tany}=...\)
\(cot\left(x-y\right)=\dfrac{1}{tan\left(x-y\right)}=\dfrac{1+tanx.tany}{tanx-tany}=...\)
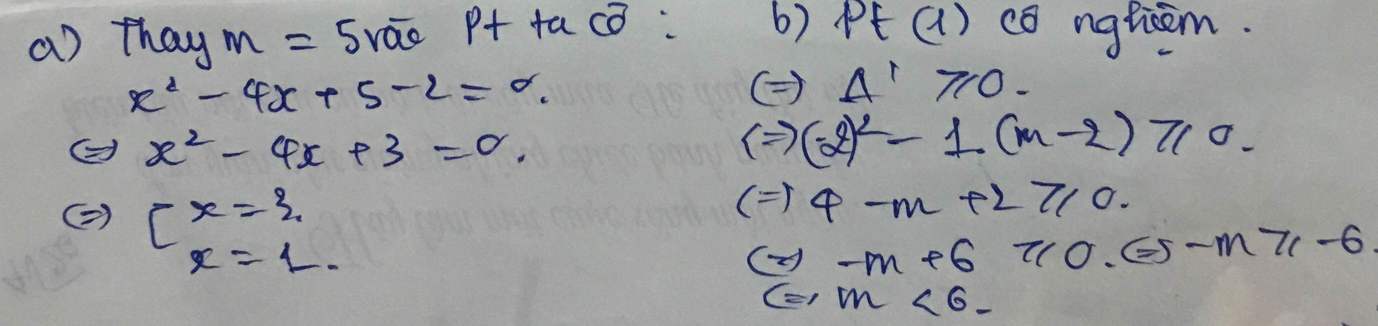
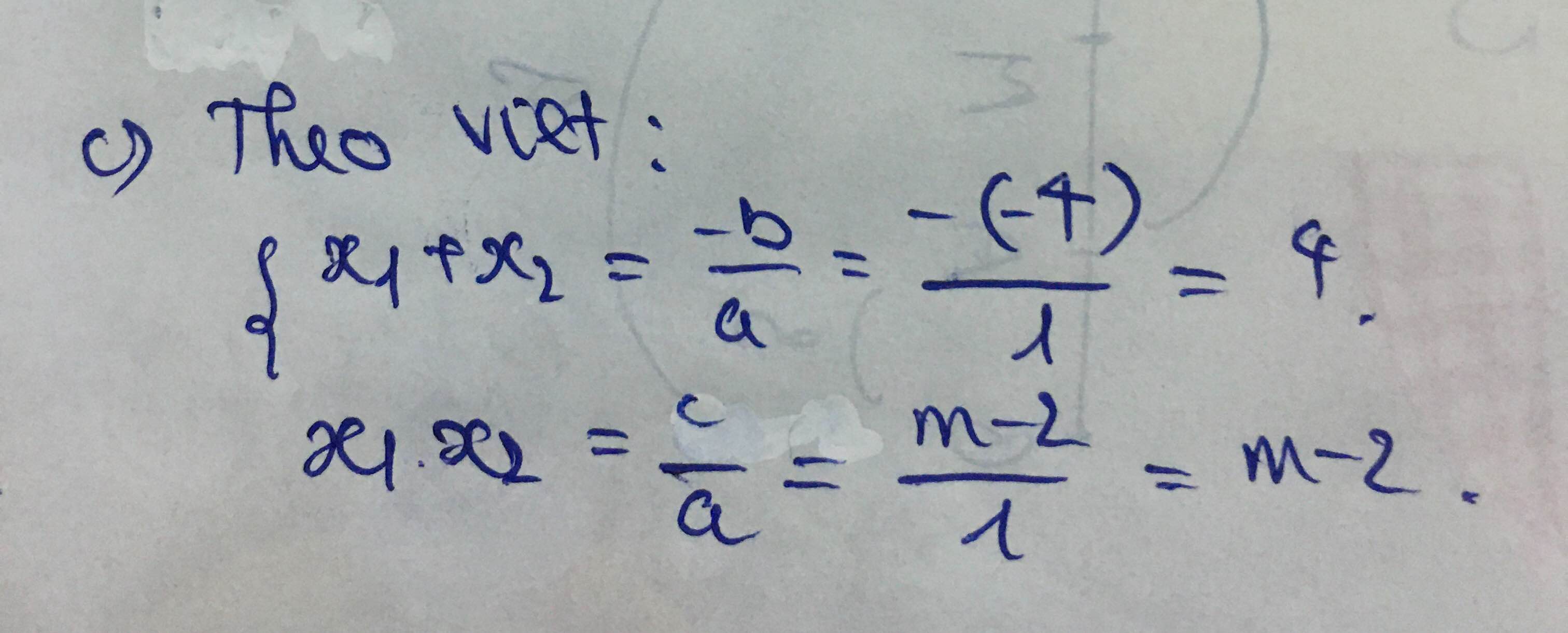
7: \(\dfrac{a}{2\sqrt{a}-1}=\dfrac{a\left(2\sqrt{a}+1\right)}{4a-1}\)
9: \(\dfrac{1}{\sqrt{a}+\sqrt{a+1}}=\dfrac{\sqrt{a+1}-\sqrt{a}}{a+1-a}=\sqrt{a+1}-\sqrt{a}\)