Bài 2: cho hình bình hành ABCD. Gọi E và F lần lượt là trung điểm của các cạnh AB và CD. Chứng minh BF=DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 8:
a: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi

a Xét tứ giác DEBF có
BE//DF
BE=FD
Do đó; DEBF là hình bình hành
=>DB cắt EF tại trung điểm của mỗi đường(1)
b: Vì ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mõi đường(2)
Từ (1), (2) suy ra AC,BD,EF đồng quy
=>E,O,F thẳng hàng

câu a: áp dụng "Tứ giác có 1 cặp cạnh đối song song và bằng nhau là hình bình hành"
Câu b: Áp dụng t/c như câu a chứng minh các tứ giác chứa các đoạn thẳng cần c/m bằng nhau ;à hình bình hành từ đó áp dụng t/c "Trong hình bình hành các cặp cạnh đối bằng nhau"
https://onlinemath.vn/cau-hoi/viet-1-doan-van-tong-phan-hop-khoang-12-cau-phan-tich-kho-tho-thu-2-bai-que-huong-trong-do-su-dung-1-cau-cam-than-vs-cau-ghep-chi-ro.8109170456376

a: BE=AB/2
DF=DC/2
mà AB=DC
nên BE=DF
Xét tứ giác BEDF có
BE//DF
BE=DF
=>BEDF là hình bình hành
=>DE=BF
b: BEDF là hbh
=>BD cắt EF tại trung điểm của mỗi đường(1)
ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AC,BD,EF đồng quy

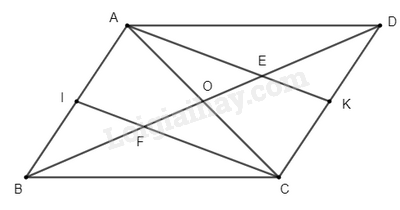
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\), \(AD\) // \(BC\); \(AB = CD\); \(AD = BC\)
Mà \(IA = IB = \frac{{AB}}{2}\); \(KD = KC = \frac{{CD}}{2}\) (do \(I\),\(K\) là trung điểm)
Suy ra \(IA = IB = KD = KC\)
Xét tứ giác \(AKCI\) có:
\(AI = KC\) (cmt)
\(AI\) // \(KC\)
Suy ra \(AKCI\) là hình bình hành
Suy ra \(IC\) // \(AK\)
Hay \(IF\) // \(AE\)
Suy ra \(AEFI\) là hình thang
b) Vì \(ABCD\), \(AKCI\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\), \(KI\)
Suy ra \(OD = OB = \frac{1}{2}BD\) (1)
Xét tam giác \(ADC\) có hai trung tuyến \(AK\), \(DO\) cắt nhau tại \(E\)
Suy ra \(E\) là trọng tâm của tam giác
Suy ra \(ED = \frac{2}{3}DO\) (2)
Chứng minh tương tự ta có \(BF = \frac{2}{3}BO\) (3)
Từ (1), (2), (3) suy ra \(ED = BF = \frac{1}{3}BD\)
Suy ra \({\rm{EF}} = \frac{1}{3}BD\)
Vậy \(DE = EF = FB\)
ABCD là hình bình hành\(\Rightarrow\left\{{}\begin{matrix}AB=CD\\AB//CD\end{matrix}\right.\)
\(AB//CD\Rightarrow BE//DF\)
E, F lần lượt là trung điểm của các cạnh AB,CD\(\Rightarrow\left\{{}\begin{matrix}BE=\dfrac{1}{2}AB\\DF=\dfrac{1}{2}DC\end{matrix}\right.\Rightarrow BE=DF\) (do AB = CD)
Xét tứ giác BEDF có BE // DF, BE = DF
\(\Rightarrow BEDF\) là hình bình hành \(\Rightarrow BF=DE\)