Biết rằng sin(18)=a+b căn5/c, với a,b,c thuộc Z , c khác 0 và a/c,b/c là các phân số tối giản. Giá trị của biểu thức S=a+b+c
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A.
Ta có
F x = ∫ 3 x 2 + 1 2 x + 1 d x = x 3 + 1 2 ln 2 x + 1 + C
mà F 0 = 0 ⇒ C = 0
Do đó
F x = x 3 + 1 2 ln 2 x + 1 ⇒ F 1 = 1 + 1 2 ln 3 ⇒ a = 1 ; b = 1 ; c = 2 ⇒ a + b + c = 4 .

 .
.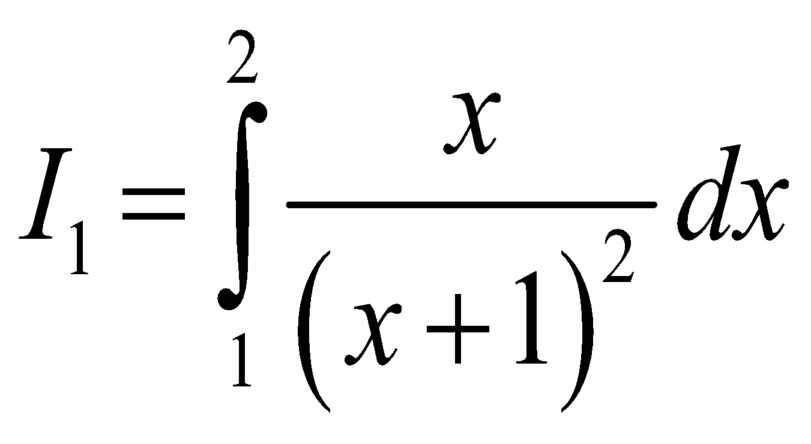 .
.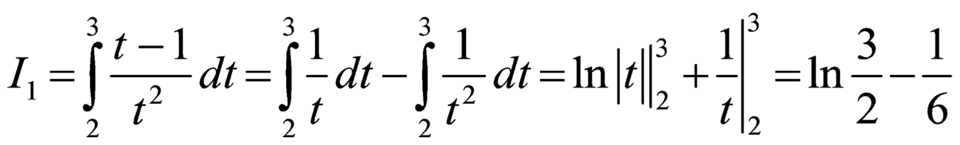 .
.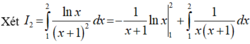
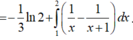
 .
.
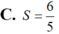



Ta có:
\(sin18^0=cos72^0=2cos^236^0-1\)
\(cos36^0=1-2sin^218^0\)
Đặt \(sin18^0=x\), \(x\in\left(0;1\right)\) thì ta có:
\(x=2\left(1-2x^2\right)^2-1\)
\(\Leftrightarrow x=2\left(4x^4-4x^2+1\right)-1\)
\(\Leftrightarrow8x^4-8x^2-x+1=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+1\right)\left(x-\dfrac{-1+\sqrt{5}}{4}\right)\left(x-\dfrac{-1-\sqrt{5}}{4}\right)=0\)
Do \(x\in\left(0;1\right)\) nên \(x=\dfrac{-1+\sqrt{5}}{4}\) \(\Rightarrow S=a+b+c=-1+1+4=4\)