(a^2-căn a/a+căn a+1) - (a^2+căn a/a^2-căn a +1) với 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2021
a) \(\dfrac{1+\sqrt{a}}{1-\sqrt{a}}=\dfrac{a+2\sqrt{a}+1}{1-a}\)
b) \(\dfrac{a-2\sqrt{a}}{2-\sqrt{a}}=\dfrac{-\sqrt{a}\left(2-\sqrt{a}\right)}{2-\sqrt{a}}=-\sqrt{a}\)
a) \(\dfrac{a}{3\sqrt{a}-1}=\dfrac{a\left(3\sqrt{a}+1\right)}{9a-1}\)
X
27 tháng 8 2019
Bài 1:
a. \(\sqrt{\frac{25m^2}{49}}=\frac{\sqrt{25m^2}}{\sqrt{49}}=\frac{5m}{7}\)
b. \(\frac{\sqrt{192k}}{\sqrt{3k}}=\sqrt{\frac{192k}{3k}}=\sqrt{64}=8\)
Bài 2:
a. \(\frac{a+\sqrt{a}}{\sqrt{a}}=\frac{\left(\sqrt{a}\right)^2+\sqrt{a}}{\sqrt{a}}=\frac{\sqrt{a}\left(\sqrt{a}+1\right)}{\sqrt{a}}=\sqrt{a}+1\)
b. \(\frac{\sqrt{a}-a}{\sqrt{a}-1}=\frac{\sqrt{a}-\left(\sqrt{a}\right)^2}{\sqrt{a}-1}=\frac{\sqrt{a}\left(1-\sqrt{a}\right)}{\sqrt{a}-1}=\frac{-\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}=-\sqrt{a}\)
c. \(\frac{a-b}{\sqrt{a}-\sqrt{b}}=\frac{\left(\sqrt{a}\right)^2-\left(\sqrt{b}\right)^2}{\sqrt{a}-\sqrt{b}}=\frac{\left(\sqrt{a}+\sqrt{b}\right)\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}=\sqrt{a}+\sqrt{b}\)
L
1
TA
3 tháng 8 2021
\(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right).\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2\\ =\left(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}{1-\sqrt{a}}+\sqrt{a}\right).\left(\dfrac{1-\sqrt{a}}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}\right)^2\\ =\left(1+2\sqrt{a}+a\right).\dfrac{1}{\left(1+\sqrt{a}\right)^2}\\ =\left(1+\sqrt{a}\right)^2.\dfrac{1}{\left(1+\sqrt{a}\right)^2}=1\)
ND
Nguyễn Đức Trí
VIP
25 tháng 8 2023
a) \(\sqrt[]{x^2-4x+4}=x+3\)
\(\Leftrightarrow\sqrt[]{\left(x-2\right)^2}=x+3\)
\(\Leftrightarrow\left|x-2\right|=x+3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=x+3\\x-2=-\left(x+3\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}0x=5\left(loại\right)\\x-2=-x-3\end{matrix}\right.\)
\(\Leftrightarrow2x=-1\Leftrightarrow x=-\dfrac{1}{2}\)
b) \(2x^2-\sqrt[]{9x^2-6x+1}=5\)
\(\Leftrightarrow2x^2-\sqrt[]{\left(3x-1\right)^2}=5\)
\(\Leftrightarrow2x^2-\left|3x-1\right|=5\)
\(\Leftrightarrow\left|3x-1\right|=2x^2-5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=2x^2-5\\3x-1=-2x^2+5\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x^2-3x-4=0\left(1\right)\\2x^2+3x-6=0\left(2\right)\end{matrix}\right.\)
Giải pt (1)
\(\Delta=9+32=41>0\)
Pt \(\left(1\right)\) \(\Leftrightarrow x=\dfrac{3\pm\sqrt[]{41}}{4}\)
Giải pt (2)
\(\Delta=9+48=57>0\)
Pt \(\left(2\right)\) \(\Leftrightarrow x=\dfrac{-3\pm\sqrt[]{57}}{4}\)
Vậy nghiệm pt là \(\left[{}\begin{matrix}x=\dfrac{3\pm\sqrt[]{41}}{4}\\x=\dfrac{-3\pm\sqrt[]{57}}{4}\end{matrix}\right.\)
27 tháng 12 2017
a)
\(7\sqrt{12}+\frac{1}{3}\sqrt{27}-\sqrt{75}\)
\(=14\sqrt{3}+\sqrt{3}-5\sqrt{3}\)
\(=10\sqrt{3}\)
b)
\(\left(2\sqrt{20}+\sqrt{125}-3\sqrt{80}\right):5\)
\(=\left(4\sqrt{5}+5\sqrt{5}-12\sqrt{5}\right):5\)
\(=-3\sqrt{5}:5\)
\(=\frac{-3\sqrt{5}}{5}\)
c)
\(3\sqrt{12a}-5\sqrt{3a}+\sqrt{48a}\)
\(=6\sqrt{3a}-5\sqrt{3a}+4\sqrt{3a}\)
\(=5\sqrt{3a}\)
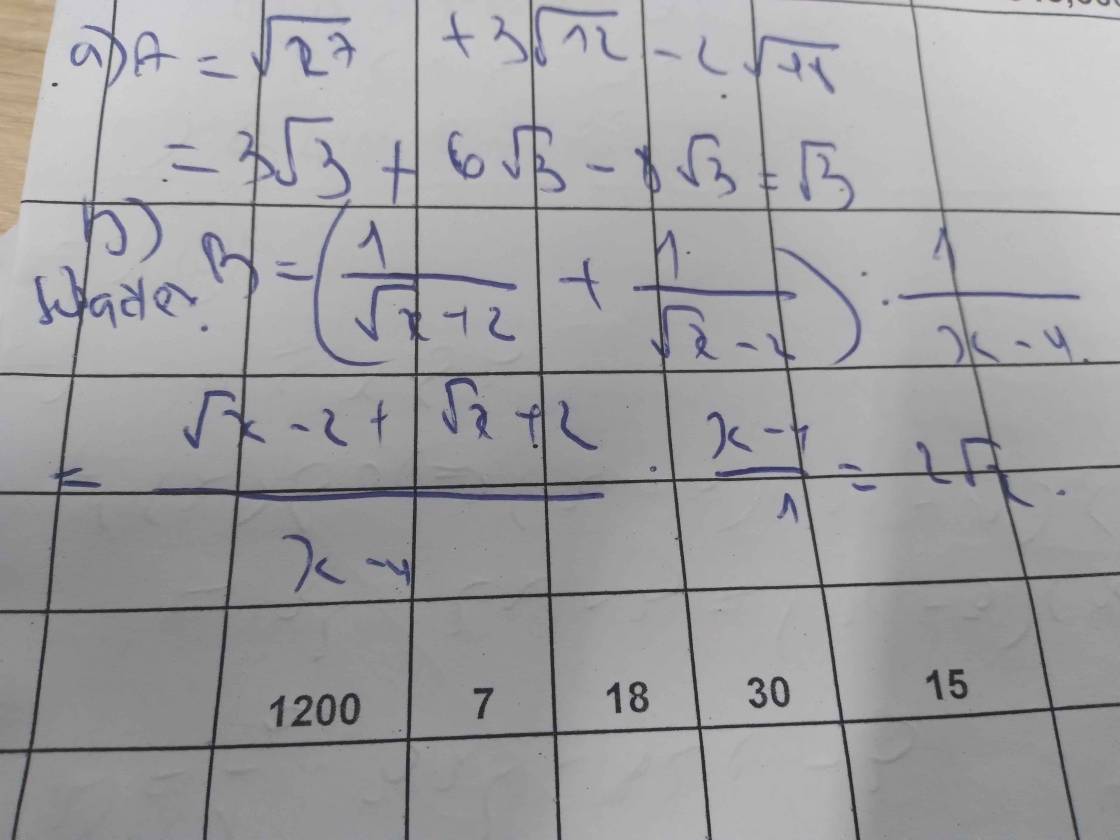
Sửa đề: a-căn a+1\(=\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{a+\sqrt{a}+1}-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{a-\sqrt{a}+1}\)
=a-căn a-a-căn a
=-2căn a