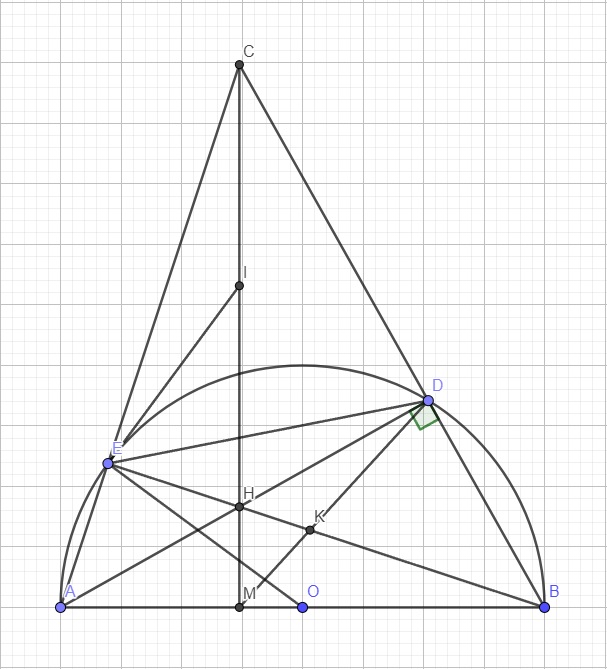
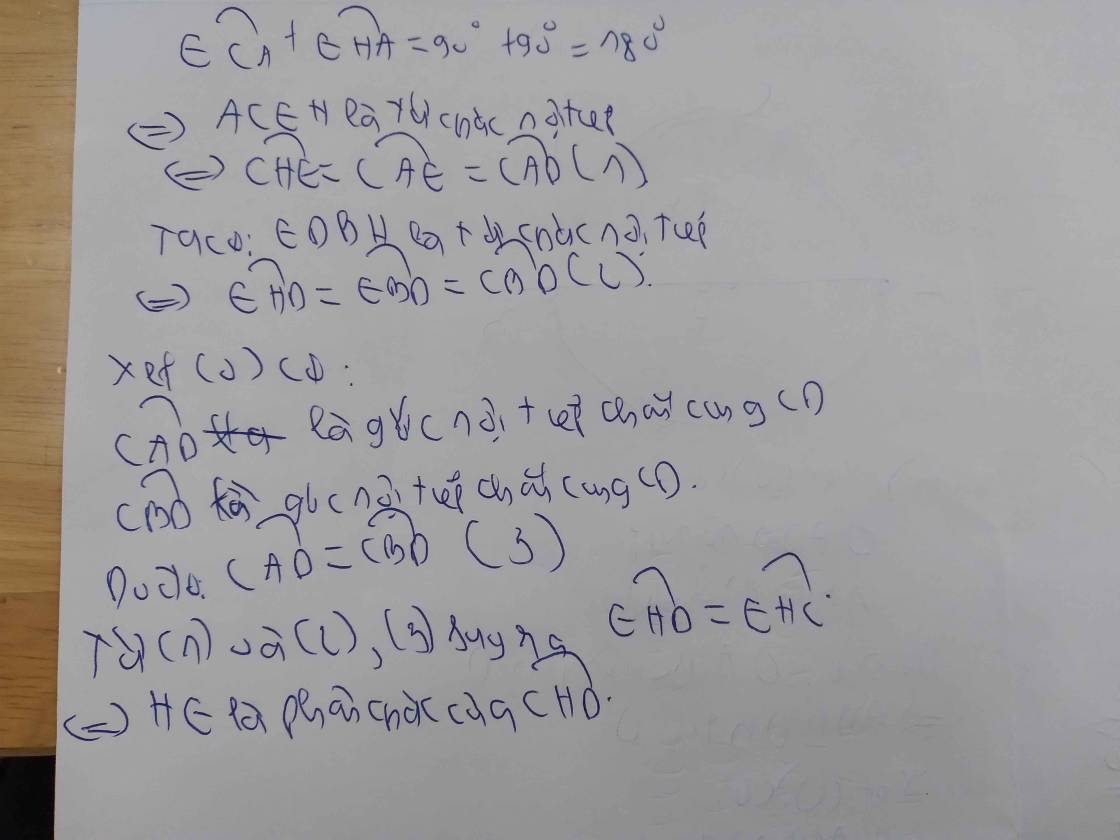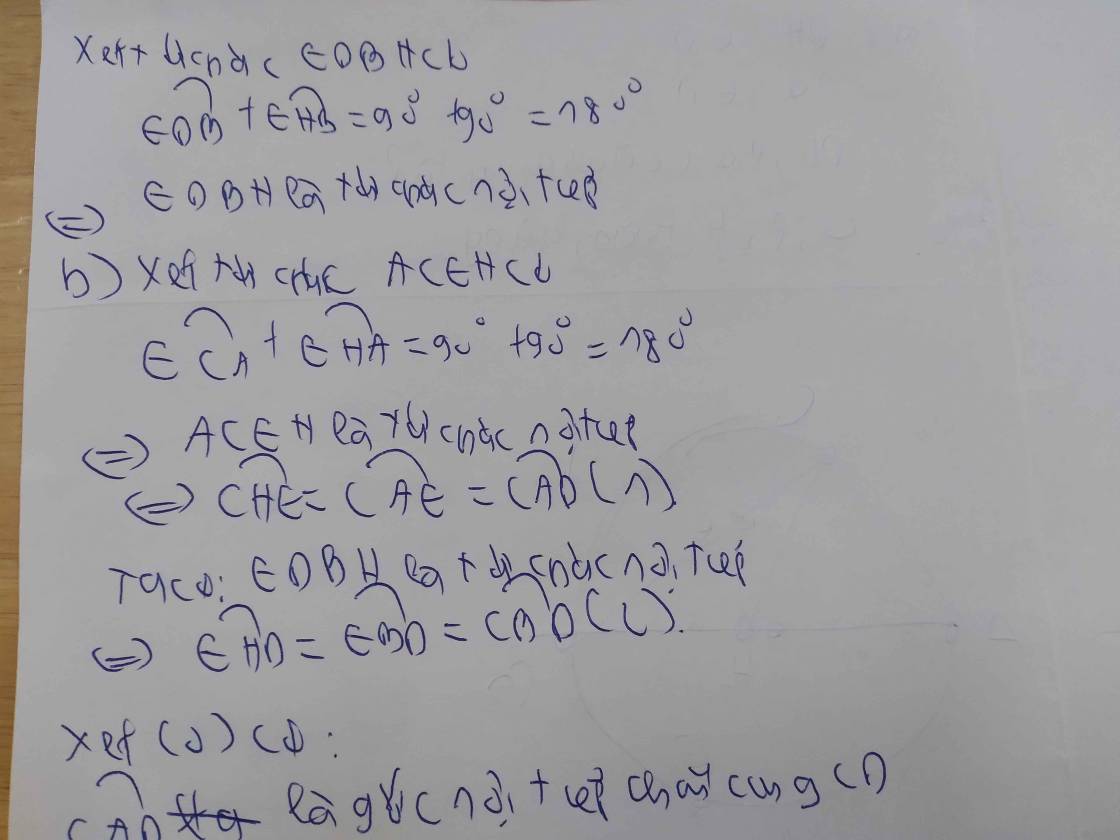Trên nửa đường tròn (O) đường kính AB, lấy điểm C trên cung AB (C khác A và B), Gọi E là điểm chính giữa cung AC, H là giao của AC và BE, D là giao điểm của AE và BC
a. Chứng minh tứ giác DEHC nội tiếp
b. Chứng minh DH vuông góc với AB
c. Chứng minh E là trung điểm của AD
d. Giả sử đường tròn đã cho là cố định và điểm C chuyển động trên nửa đường tròn đó. CMR điểm D chuyển động trên 1 cung tròn cố định