Vật sáng AB đặt trước thấu kính phân kỳ có tiêu cự -20cm cho ảnh A'B' cách vật 10cm. Khoảng cách từ vật đến thấu kính là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sơ đồ tạo ảnh:

Vật sáng AB là một đoạn thẳng đặt vuông góc với trục chính của thấu kính cho ảnh cao bằng vật
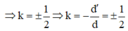
Tuy nhiên vật thật qua thấu kính hội tụ luôn cho ảnh ảo nhỏ hơn vật nên trong bài toán này ta chỉ lấy
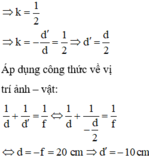

Sơ đồ tạo ảnh:

Áp dụng công thức về vị trí ảnh – vật:

Như vậy k > 0 nên ảnh cùng chiều với vật cao bằng một phần ba vật.

Bài 2.
Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\)
\(\Rightarrow d'=60cm\)
Chiều cao ảnh: \(\dfrac{h}{h'}=\dfrac{d}{d'}\)
\(\Rightarrow\dfrac{1,5}{h'}=\dfrac{30}{60}\Rightarrow h'=3cm\)

Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 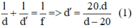
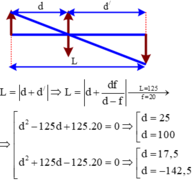
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 125cm
∗ Trường hợp 1: A’B’ là ảnh thật → d’ > 0
→ L = d’ + d =125cm (2)
Từ (1) và (2) ta có:
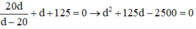
Giải phương trình lấy nghiệm d1 > 0 ta được: d1 = 17,54 cm
∗ Trường hợp 2
d’ + d = - 125cm (trường hợp này thì ảnh A’B’ là ảnh ảo) (3)
Từ (1) và (3) ta có:
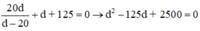
Giải phương trình lấy nghiệm d > 0 ta được: d = 25cm hoặc d = 100cm

Sơ đồ tạo ảnh
AB → A’B’
d d’
Công thức thấu kính: 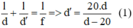
Gọi khoảng cách từ vật tới ảnh là L ⇒ |d’ + d| = L.
Vật thật ⇒ d > 0
L = 45cm
∗ Trường hợp 1
d’ + d = -45cm (2)
Từ (1) và (2) ta có:
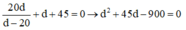
Giải phương trình lấy nghiệm d > 0 ta được: d = 15 cm
∗ Trường hợp 2
d’ + d = 45cm (3)
Từ (1) và (3) ta có:
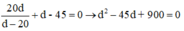
phương trình này vô nghiệm
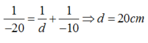
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow-\dfrac{1}{20}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(d-\left|d'\right|=10\Leftrightarrow d+d'=10\left(d'< 0\right)\)
\(\Rightarrow d=\dfrac{d'f}{d'-f}=\dfrac{-20.\left(10-d\right)}{10-d+20}=\dfrac{20d-200}{30-d}\Leftrightarrow30d-d^2=20d-200\Leftrightarrow d=...\left(cm\right)\)