cho a>b ,hãy so sánh -4a 2018 và -4b 2019
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YT
25 tháng 3 2018
a<b
suy ra-4a<-4b
suy ra2016-4a<2016-4b
ma 2016-4b<2017-4b
vay 2016-4a,<2017-4b
25 tháng 3 2018
Ta có: a > b
khi nhân cả 2 vế vs -4
=> -4a < -4b
Cộng cả 2 vế với 2016:
=> 2016 - 4a < 2016 - 4b (1)
Ta có: 2016 < 2017
Khi Cộng cả 2 vế vs -4b
=> 2016 - 4b < 2017 - 4b (2)
Từ (1) và (2) => 2016 - 4a < 2017 - 4b
NN
24 tháng 4 2019
a) Ta có: a>b => 2a > 2b (nhân 2 vế với 2)
=> 2a - 3 > 2b - 3 (cộng 2 vế với -3)
b) Ta có: -4a+1 < -4b+ 1 => -4a < -4b ( cộng 2 vế với -1)
=> a > b (nhân 2 vế với -1/4)
c) Ta có: 3-4a < 5c+2 => 3-4a-3 < 5c+2-3 (cộng 2 vế với -3)
=> -4a < 5c-1
Mà 5c-1 < -4b nên -4a < -4b => a > b (nhân cả 2 vế với -1/4)
CA
1
H
1
NH
11 tháng 5 2019
\(A=\frac{2018^{2019}-1}{2018^{2019}+1}=\frac{2018^{2019}+1-2}{2018^{2019}+1}=\frac{2018^{2019}+1}{2018^{2019}+1}-\frac{2}{2018^{2019}+1}=1-\frac{2}{2018^{2019}+1}\)
\(B=\frac{2018^{2019}}{2018^{2019}+2}=\frac{2018^{2019}+2-2}{2018^{2019}+2}=\frac{2018^{2019}+2}{2018^{2019}+2}-\frac{2}{2018^{2019}+2}=1-\frac{2}{2018^{2019}+2}\)
Ta có: \(\frac{2}{2018^{2019}+1}>\frac{2}{2018^{2019}+2}\)
\(\Rightarrow1-\frac{2}{2018^{2019}+1}< 1-\frac{2}{2018^{2019}+2}\)
\(\Rightarrow A< B\)
Vậy .....
25 tháng 5 2022
tham khảo
4a + 5 < 4b+5
<=> 4a +5 - 5 < 4b+5 - 5
<=> 4a < 4b
<=> a < b
ET
1
H
12 tháng 4 2018
Ta có : \(0< \frac{2017}{2018}< 1\) nên \(\frac{2017}{2018}>\frac{2017+2019}{2018+2019}\)(1)
\(0< \frac{2018}{2019}< 1\) nên \(\frac{2018}{2019}>\frac{2018+2018}{2018+2019}\) (2)
Cộng vế theo vế 1 và 2 ta được : \(B=\frac{2017}{2018}+\frac{2018}{2019}>\frac{2017+2018+2018+2019}{2018+2019}=\frac{2017+2018}{2018 +2019}+1=A+1>A\)
Vậy B>A
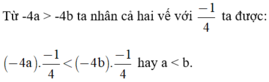
-4a2018<-4b2019 vì số âm có giá trị tuyệt đối càng lớn thì càng nhỏ nhé
`a>b`
`<=>-a<-b`
`<=>-4a<-4b`
`<=>-4a-2018<-4b-2018<-4b-2019`