Một cái ly giấy loại 22 oz (oz là đơn vị đo thể tích ở châu Âu, 1 oz = 29,5 ml) loại nón cụt có đường kính miệng là 90 mm, cao 156 mm. a) Tính đường kính mặt đáy của ly. Cho pi = 3,14 và làm tròn đến hàng đơn vị.b) Anh Bình mua 3500 cái ly giấy loại 22 oz như thế thì phải trả bao nhiêu tiền theo bảng dưới đây (biết cty này chỉ bán 500 cái trở...
Đọc tiếp
Một cái ly giấy loại 22 oz (oz là đơn vị đo thể tích ở châu Âu, 1 oz = 29,5 ml) loại nón cụt có đường kính miệng là 90 mm, cao 156 mm.
a) Tính đường kính mặt đáy của ly. Cho pi = 3,14 và làm tròn đến hàng đơn vị.
b) Anh Bình mua 3500 cái ly giấy loại 22 oz như thế thì phải trả bao nhiêu tiền theo bảng dưới đây (biết cty này chỉ bán 500 cái trở lên)
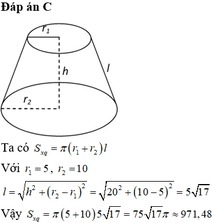
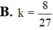
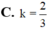
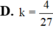
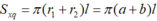
\(d_1=90mm\Rightarrow r_1=\dfrac{90}{2}=45mm\)
\(h=156mm\)
\(1oz\) có thể tích là \(29,5ml=29500mm^3\) \(\Rightarrow22oz=295.22=64900mm^3\)
Ta có : \(V_{ly}=\dfrac{1}{3}\pi\left(r_1^2+r_2^2+r_1r_2\right)h\)
\(\Leftrightarrow64900=\dfrac{1}{3}.3,14\left(45^2+r_2^2+45r_2\right)156\)
\(\Leftrightarrow64900=163,28\left(2025+r_2^2+45r_2\right)\)
\(\Leftrightarrow397\approx2025+r_2^2+45r_2\)
\(\Leftrightarrow r_2^2+45r_2-1628=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}r_2\approx24\left(n\right)\\r_2\approx-69\left(l\right)\end{matrix}\right.\)
Đường kính đáy là : \(24.2=48\left(mm\right)\)
\(3500\) ly nằm trong số lượng : Từ \(2000-4999:1065d\)
Vậy 3500 ly thì phải trả số tien là : \(3500.1065=3727500\left(d\right)\)