Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D
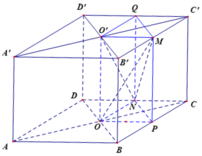
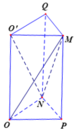
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có S ∆ O P N = 1 4 S ∆ B C D = 1 8 S A B C D = a 2 8 ⇒ V O P N . O ' M Q = a 3 8
mà
V O O ' M N = V O P N . O ' M Q - V M . O P N - V N . O ' M Q = a 3 8 - 1 3 . a 3 8 - 1 3 . a 3 8 = a 3 24
a) Chứng minh B 1 , C 1 , D 1 lần lượt là trung điểm của các cạnh SB, SC, SD
Ta có:
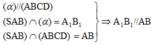
⇒ A 1 B 1 là đường trung bình của tam giác SAB.
⇒ B 1 là trung điểm của SB (đpcm)
*Chứng minh tương tự ta cũng được:
• C 1 là trung điểm của SC.
• D 1 là trung điểm của SD.
b) Chứng minh B 1 B 2 = B 2 B , C 1 C 2 = C 2 C , D 1 D 2 = D 2 D .
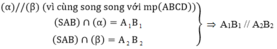
⇒ A 2 B 2 là đường trung bình của hình thang A 1 B 1 B A
⇒ B 2 là trung điểm của B 1 B
⇒ B 1 B 2 = B 2 B (đpcm)
*Chứng minh tương tự ta cũng được:
• C 2 là trung điểm của C 1 C 2 ⇒ C 1 C 2 = C 2 C
• D 2 là trung điểm của D 1 D 2 ⇒ D 1 D 2 = D 2 D .
c) Các hình chóp cụt có một đáy là tứ giác ABCD, đó là : A 1 B 1 C 1 D 1 . A B C D v à A 2 B 2 C 2 D 2 . A B C D
Đáp án D
S O ' O N = 1 2 OO'.ON= 1 2 . a . a 2 = a 2 4 ; M O ' = a 2 . V M O ' O N = 1 3 M O ' . S O ' O N = a 3 24 .
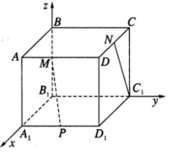
Ta chọn hệ trục tọa độ như sau: B 1 là gốc tọa độ, B 1 A 1 → = i → , B 1 C 1 → = j → , B 1 B → = k → . Trong hệ trục vừa chọn, ta có B 1 (0; 0; 0), B(0; 0; 1), A 1 (1; 0; 0), D 1 (1; 1; 0), C(0; 1; 1), D(1; 1; 1), C 1 (0; 1; 0).
Suy ra M(0; 0; 1/2), P(1; 1/2; 0), N(1/2; 1; 1)
Ta có MP → = (1; 1/2; −1/2); C 1 N → = (1/2; 0; 1)
Gọi ( α ) là mặt phẳng chứa C 1 N và song song với MP. ( α ) có vecto pháp tuyến là n → = (1/2; −5/4; −14) hay n ' → = (2; −5; −1)
Phương trình của ( α ) là 2x – 5(y – 1) – z = 0 hay 2x – 5y – z + 5 = 0
Ta có:
d(MP,
C
1
N) = d(M,(
α
)) 
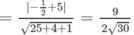
Ta có:
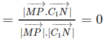
Vậy ∠ (MP, C 1 N) = 90 ° .
