Bạn Phương phân tích đa thức sau thành nhân tử, hãy xác định Bạn Phương làm như vậy là đúng hay sai
m(m-3)+3 = (m+3)(m-3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 10 2017
x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung
3 tháng 1 2017
Gửi Thắng Nguyễn: Mình không biết tại sao lại ko phân tích được?
CM
5 tháng 2 2017
Đáp án B
Ta thấy Lan đặt tính đúng, tuy nhiên khi tính thì bạn đã cộng số cần nhớ vào hàng trăm rồi mới tiếp tục nhân, như vậy là sai.
232 × 4 được tính đúng như sau:
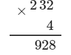
Đặt tính thẳng cột và thực hiện phép nhân:
+ 4 nhân 2 là 8, viết 8.
+ 4 nhân 3 là 12, viết 2 nhớ 1.
+ 4 nhân 2 là 8, thêm 1 bằng 9, viết 9.
Vậy kết quả của phép nhân là 928.
DD
3
CM
4 tháng 6 2017
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: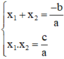 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
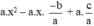
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm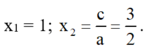 
Vậy: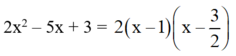 
12 tháng 7 2016
a) 2x + 2y - x2 - xy
= 2(x + y) + x(x + y)
= (x + y) (x + 2)
mk ko bít phân tích đúng ko đúng thì t i c k nhé!! 245433463463564564574675687687856856846865855476457
D
12 tháng 7 2016
a)\(2x+2y-x^2-xy=2\left(x+y\right)-x\left(x+y\right)=\left(2-x\right)\left(x+y\right)\)
b)\(\left(x+3\right)^2-\left(2x-5\right)\left(x+3\right)\)
\(=\left(x+3\right)\left[\left(x+3\right)-\left(2x-5\right)\right]\)
\(=\left(x+3\right)\left(8-x\right)\)
c)\(\left(3x+2\right)^2+\left(3x-2\right)^2-2\left(9x^2-4\right)\)
\(=\left(3x+2\right)^2+\left(3x-2\right)^2-2\left(3x-2\right)^2\)
\(=\left(3x+2\right)\left[\left(3x+2\right)-\left(3x-2\right)\right]+\left(3x-2\right)\left[\left(3x-2\right)-\left(3x+2\right)\right]\)
\(=4\left(3x+2\right)-4\left(3x-2\right)\)
\(=4\left(3x+2-3x+2\right)\)
=4.4=16
8 tháng 10 2016
25n(n-1)-50(n-1) luôn chia hết cho 150 với mọi n là số nguyên
giúp mình chứng minh nha . Cám ơn mấy bạn
Giả sử bạn Phương làm đúng thì nghiệm của đa thức:
(m+3)(m-3) cũng là nghiệm của đa thức m(m-3) + 3
(m+3)(m-3) =0 ⇒ \(\left[{}\begin{matrix}m=-3\\m=3\end{matrix}\right.\)
với m = - 3 thay vào đa thức m(m-3) + 3 ta có:
3\(\times\)( 3 - 3) + 3 = 3 \(\ne\) 0 ( trái với giả sử)
Vậy Phương làm như vậy là sai