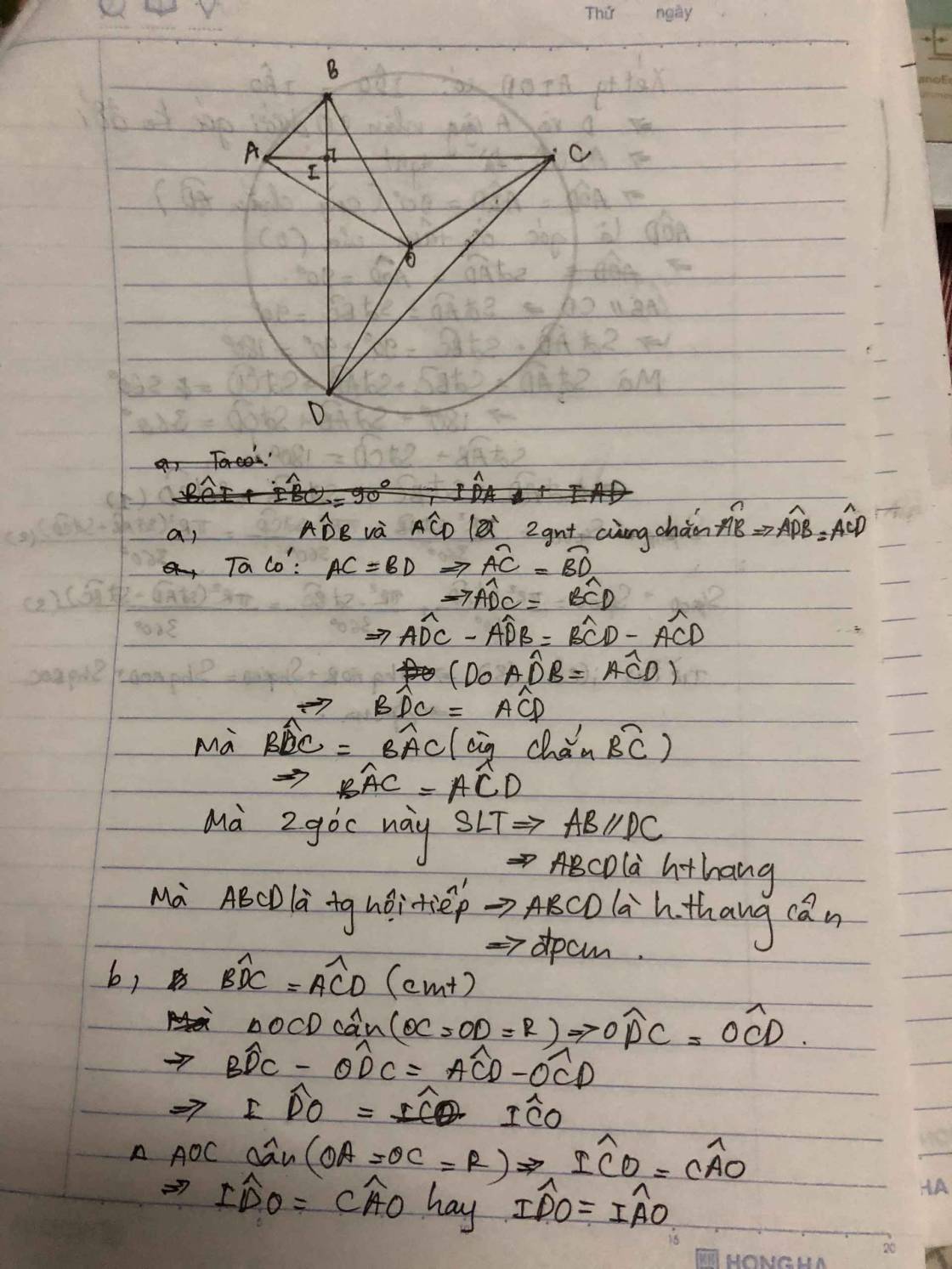cho đường tròn o , 8cm và i , 6cm cắt nhau tại hai điểm A và B biết OI bằng 10 cm tính diện tích tứ giác OAIB tính góc AOB và góc AIB tính diện tích phần tô đậm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2023
Xét hai tam giác OAI và OBI có:
\(\left\{{}\begin{matrix}OA=OB=6\\IA=IB=8\\OI\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAI=\Delta OBI\left(c.c.c\right)\)
\(\Rightarrow\widehat{OAI}=\widehat{OBI}\) (1)
Mà tứ giác OAIB nội tiếp \(\Rightarrow\widehat{OAI}+\widehat{OBI}=180^0\) (2)
(1);(2) \(\Rightarrow\widehat{OAI}=\widehat{OBI}=90^0\)
Áp dụng định lý Pitago:
\(OI=\sqrt{OA^2+IA^2}=\sqrt{6^2+8^2}=10\)
22 tháng 3 2023
a: Xét ΔOAB vuông tại O và ΔOCD vuông tại O có
góc OAB=góc OCD
=>ΔOAB đồng dạng với ΔOCD
b: Xét ΔABD vuông tại A và ΔDAC vuông tại D có
góc ABD=góc DAC
=>ΔABD đồng dạng với ΔDAC
GN
27 tháng 5 2018
B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)