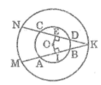
Cho dây AB của đường tròn (O;R). Các tiếp tuyến tại A và B của (O) cắt nhau tại C. Nối tâm O với điểm H thuộc dây AB và kẻ qua H đường thẳng vuông góc với OH, đường này cắt CA ở E và CB ở D.
a) Chứng minh: OBCA nội tiếp
b) Chứng minh: OA.OD=OB.OEc
) Cho AB=R √33 Tính diện tích phần mặt phẳng giới hạn bởi BC, AC và cung nhỏ AB theo R

a: góc OAC+góc OBC=180 độ
=>OACB nội tiếp
b: góc OEA+góc OHA=180 độ
=>OEAH nội tiếp
góc OBD+góc OHD=180 độ
=>OHDB nội tiếp
góc OEH=góc OAH
góc ODH=góc OBH
mà góc OAH=gócc OBH
nên góc OEH=góc ODH
=>OE=OD
=>OA*OD=OB*OE