tìm x nguyên để \(\dfrac{x-1}{x^2}\) nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2023
\(A=\dfrac{x^2+x}{x^2-2x+1}:\left(\dfrac{x+1}{x}-\dfrac{1}{1-x}+\dfrac{2-x^2}{x^2-x}\right)\left(1\right)\)
a) A xác định \(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne1\end{matrix}\right.\)
\(\left(1\right)\Rightarrow A=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right)\)
\(\Rightarrow A=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\dfrac{\left(x+1\right)\left(x-1\right)+x+2-x^2}{x\left(x-1\right)}\right)\)
\(\Rightarrow A=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\dfrac{x^2-1+x+2-x^2}{x\left(x-1\right)}\right)\)
\(\Rightarrow A=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left(\dfrac{x+1}{x\left(x-1\right)}\right)\)
\(\Rightarrow A=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}=\dfrac{x^2}{x+1}\)
b) Để \(A=-\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{x^2}{x+1}=-\dfrac{1}{2}\left(x\ne-1\right)\)
\(\Leftrightarrow2x^2=-\left(x+1\right)\)
\(\Leftrightarrow2x^2+x+1=0\)
\(\Delta=1-8=-7< 0\)
Nên phương trình trên vô nghiệm \(\left(x\in\varnothing\right)\)
c) Để \(A< 1\)
\(\Leftrightarrow\dfrac{x^2}{x+1}< 1\)
\(\Leftrightarrow x^2< x+1\left(x\ne-1\right)\)
\(\Leftrightarrow x^2-x-1< 0\)
\(\Leftrightarrow x^2-x+\dfrac{1}{4}-\dfrac{1}{4}-1< 0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2-\dfrac{5}{4}< 0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2< \dfrac{5}{4}\)
\(\Leftrightarrow-\dfrac{\sqrt[]{5}}{2}< x-\dfrac{1}{2}< \dfrac{\sqrt[]{5}}{2}\)
\(\Leftrightarrow\dfrac{-\sqrt[]{5}+1}{2}< x< \dfrac{\sqrt[]{5}+1}{2}\)
d) Để A nguyên
\(\Leftrightarrow\dfrac{x^2}{x+1}\in Z\)
\(\Leftrightarrow x^2⋮x+1\)
\(\Leftrightarrow x^2-x\left(x+1\right)⋮x+1\)
\(\Leftrightarrow x^2-x^2+x⋮x+1\)
\(\Leftrightarrow x⋮x+1\)
\(\Leftrightarrow x-x-1⋮x+1\)
\(\Leftrightarrow-1⋮x+1\)
\(\Leftrightarrow x+1\in\left\{-1;1\right\}\)
\(\Leftrightarrow x\in\left\{-2;0\right\}\left(x\in Z\right)\)
8 tháng 2 2023
a: ĐKXĐ: x<>1; x<>2; x<>-2; x<>-1
\(P=\dfrac{2017x+2017-2016x+2016-2014x-2016}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{-2015x+2017}{x^2-4}\)
27 tháng 11 2021
\(a,P=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{2}=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\\ b,P=1\Leftrightarrow\sqrt{x}+1=2\sqrt{x}\\ \Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\\ c,P=\dfrac{\sqrt{x}+1}{2\sqrt{x}}\in Z\\ \Leftrightarrow\sqrt{x}+1⋮2\sqrt{x}\\ \Leftrightarrow2\sqrt{x}+2⋮2\sqrt{x}\\ \Leftrightarrow2\sqrt{x}\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow\sqrt{x}=1\left(\sqrt{x}>0\right)\\ \Leftrightarrow x=1\)
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
Lời giải:
a. ĐKXĐ: $x\geq 0$
$P< \frac{1}{2}\Leftrightarrow \frac{\sqrt{x}}{\sqrt{x}+2}< \frac{1}{2}$
$\Leftrightarrow \frac{\sqrt{x}}{\sqrt{x}+2}-\frac{1}{2}<0$
$\Leftrightarrow \frac{\sqrt{x}-2}{2(\sqrt{x}+2)}<0$
$\Leftrightarrow \sqrt{x}-2<0$ (do mẫu dương rồi)
$\Leftrightarrow 0\leq x< 4$
Kết hợp đkxđ suy ra $0\leq x< 4$
b.
Với $x\geq 0$ thì $P\geq 0$
Lại có: $P<1$ (do tử nhỏ hơn mẫu)
$\Rightarrow P$ nguyên khi mà $P=0$
$\Leftrightarrow x=0$
29 tháng 7 2021
1) Ta có: \(P=\dfrac{1}{\sqrt{x}-1}-\dfrac{x\sqrt{x}-\sqrt{x}}{x+1}\left(\dfrac{1}{x-2\sqrt{x}+1}+\dfrac{1}{1-x}\right)\)
\(=\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}\left(x-1\right)}{x+1}\cdot\left(\dfrac{\sqrt{x}+1-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{1}{\sqrt{x}-1}-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{x+1}\cdot\dfrac{2}{\left(\sqrt{x}-1\right)^2\cdot\left(\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(x+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{x+1}\)
Để \(P=-\dfrac{2}{5}\) thì \(\dfrac{\sqrt{x}-1}{x+1}=\dfrac{-2}{5}\)
\(\Leftrightarrow-2x-2=5\sqrt{x}-5\)
\(\Leftrightarrow-2x-2-5\sqrt{x}+5=0\)
\(\Leftrightarrow-2x-5\sqrt{x}+3=0\)
\(\Leftrightarrow-2x-6\sqrt{x}+\sqrt{x}+3=0\)
\(\Leftrightarrow-2\sqrt{x}\left(\sqrt{x}+3\right)+\left(\sqrt{x}+3\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}+3\right)\left(-2\sqrt{x}+1\right)=0\)
\(\Leftrightarrow-2\sqrt{x}+1=0\)
\(\Leftrightarrow-2\sqrt{x}=-1\)
\(\Leftrightarrow x=\dfrac{1}{4}\)(thỏa ĐK)
1 tháng 5 2022
ĐKXĐ: \(x\ne\pm1;x\ne0\)
a)\(\left(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}\right):\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)
\(=\left(\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\right):\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)
\(=\dfrac{x^2+2x+1-\left(x^2-2x+1\right)}{\left(x-1\right)\left(x+1\right)}:\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)
\(=\dfrac{4x}{\left(x-1\right)\left(x+1\right)}:\dfrac{2x}{5x-5}-\dfrac{x^2-1}{x^2+2x+1}\)
\(=\dfrac{4x}{\left(x-1\right)\left(x+1\right)}.\dfrac{5\left(x-1\right)}{2x}-\dfrac{x^2-1}{x^2+2x+1}\)
\(=\dfrac{10}{x+1}-\dfrac{\left(x+1\right)\left(x-1\right)}{\left(x+1\right)^2}\)
\(=\dfrac{10}{x+1}-\dfrac{x-1}{x+1}\)
\(=\dfrac{11-x}{x+1}\)
b) \(A=\dfrac{11-x}{x+1}=2\)
\(\Leftrightarrow11-x=2\left(x+1\right)\)
\(\Leftrightarrow11-x=2x+2\)
\(\Leftrightarrow-x-2x=2-11\)
\(\Leftrightarrow-3x=-9\)
\(\Leftrightarrow x=3\left(nhận\right)\)
c) -Để \(A=\dfrac{11-x}{x+1}\in Z\) thì:
\(\left(11-x\right)⋮\left(x+1\right)\)
\(\Rightarrow\left(12-x-1\right)⋮\left(x+1\right)\)
\(\Rightarrow12⋮\left(x+1\right)\)
\(\Rightarrow\left(x+1\right)\inƯ\left(12\right)\)
\(\Rightarrow\left(x+1\right)\in\left\{1;2;3;4;6;12;-1;-2;-3;-4;-6;-12\right\}\)
\(\Rightarrow x\in\left\{2;3;5;11;-2;-3;-4;-5;-7;-13\right\}\)
DX
26 tháng 2 2023
\(A=\left(\dfrac{x}{x^2-4}+\dfrac{2}{2-x}+\dfrac{1}{x+2}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(\Rightarrow A=\left(\dfrac{x-2\left(x+2\right)+1\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\right):\left(\dfrac{\left(x-2\right)\left(x+2\right)+10-x^2}{x+2}\right)\)
\(\Rightarrow A=\left(\dfrac{-6}{x^2-4}\right):\left(\dfrac{6}{x+2}\right)\)
\(\Rightarrow A=-\dfrac{6}{x^2-4}.\dfrac{x+2}{6}=-\dfrac{6\left(x+2\right)}{\left(x-2\right)\left(x+2\right)6}=-\dfrac{1}{x-2}\)
để A<0 thì :
\(\left\{{}\begin{matrix}x-2\ne0\\x-2\notin Z-\end{matrix}\right.\)\(\Leftrightarrow x\in\left\{3;4;5;6;7;8;9;....n\right\}\)
( Z- là tập hợp số nguyên âm )
Để A có giá trị nguyên thì :
\(\left\{{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
3 tháng 3 2022
a, ĐKXĐ:\(\left\{{}\begin{matrix}x+3\ne0\\x^2+x-6\ne0\\2-x\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-3\\x^2+x-6\ne0\\x\ne2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-3\\x\ne2\end{matrix}\right.\)
b, \(A=\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}+\dfrac{1}{2-x}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+3\right)}-\dfrac{5}{\left(x-2\right)\left(x+3\right)}-\dfrac{x+3}{\left(x-2\right)\left(x+3\right)}\)
\(=\dfrac{x^2-4-5-x-3}{\left(x-2\right)\left(x+3\right)}\)
\(=\dfrac{x^2-x-12}{\left(x-2\right)\left(x+3\right)}\)
\(=\dfrac{\left(x-4\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}\)
\(=\dfrac{x-4}{x-2}\)
\(c,A=\dfrac{-3}{4}\\ \Leftrightarrow\dfrac{x-4}{x-2}=\dfrac{-3}{4}\\ \Leftrightarrow4\left(x-4\right)=-3\left(x-2\right)\\ \Leftrightarrow4x-16x=-3x+6\\ \Leftrightarrow4x-16x+3x-6=0\\ \Leftrightarrow7x-22=0\\ \Leftrightarrow x=\dfrac{22}{7}\)
d, \(A=\dfrac{x-4}{x-2}=\dfrac{x-2-2}{x-2}=1-\dfrac{2}{x-2}\)
Để \(A\in Z\Rightarrow\dfrac{2}{x-2}\in Z\Rightarrow x-2\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\)
Ta có bảng:
| x-2 | -2 | -1 | 1 | 2 |
| x | 0 | 1 | 3 | 4 |
Vậy \(x\in\left\{0;1;3;4\right\}\)
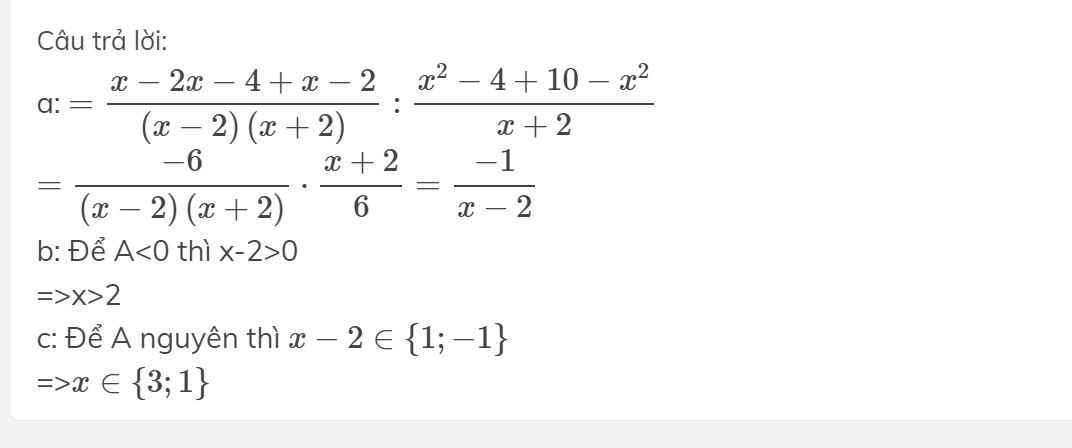
Để A nguyên thì x-1 chia hết cho x^2
=>x^2-1 chia hết cho x^2
=>-1 chia hết cho x^2
=>x=1 hoặc x=-1