Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, SA L (ABCD), SB tạo với đáy một góc 45°. Tính khoảng cách giữa AB và SD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là D
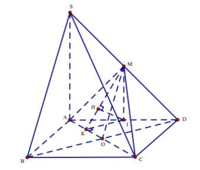
+ Gọi O là giao điểm của AC,BD
⇒ MO \\ SB ⇒ SB \\ ACM
⇒ d SB,ACM = d B,ACM = d D,ACM .
+ Gọi I là trung điểm của AD ,
M I \ \ S A ⇒ M I ⊥ A B C D d D , A C M = 2 d I , A C M .
+ Trong ABCD: IK ⊥ AC (với K ∈ AC ).
+ Trong MIK: IH ⊥ MK (với H ∈ MK ) (1) .
+ Ta có: AC ⊥ MI ,AC ⊥ IK ⇒ AC ⊥ MIK
⇒ AC ⊥ IH (2) .
Từ 1 và 2 suy ra
IH ⊥ ACM ⇒ d I ,ACM = IH .
+ Tính IH ?
- Trong tam giác vuông MIK. : I H = I M . I K I M 2 + I K 2 .
- Mặt khác: M I = S A 2 = a , I K = O D 2 = B D 4 = a 2 4
⇒ I H = a a 2 4 a 2 + a 2 8 = a 3
Vậy d S B , A C M = 2 a 3 .
Lời giải khác
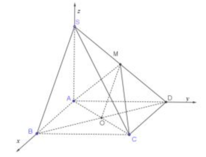

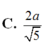
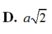
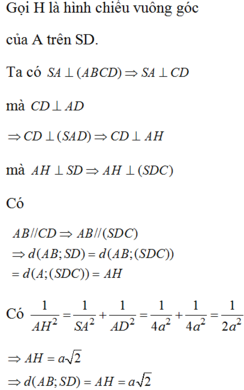
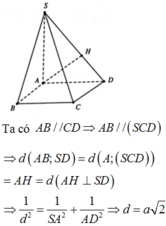
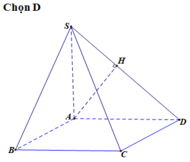


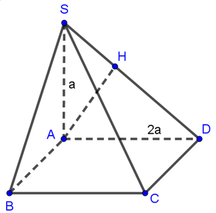

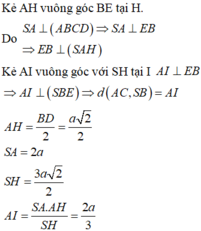
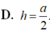
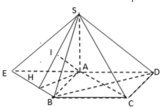

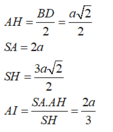
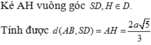
Sửa đề: SC tạo với đáy góc 45 độ
(SC;(ABCD))=45 độ
=>(CS;CA)=45 độ
=>góc SCA=45 độ
\(AC=\sqrt{2\cdot AB^2}=2a\sqrt{2}\)
=>SA=2a*căn 2
=>\(SC=\sqrt{2\cdot SA^2}=4a\)
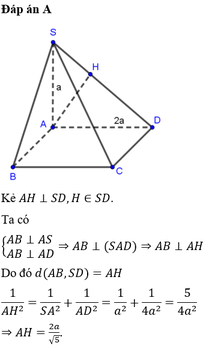
Kẻ AH vuông góc SD
CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>CD vuông góc AH
=>AH vuông góc (SCD)
=>d(A;(SCD))=AH
\(SD=\sqrt{SA^2+AD^2}=2\sqrt{3}\cdot a\)
=>\(AH=\dfrac{2\sqrt{6}}{3}a\)
AH vuông góc SD
AB vuông góc AH
=>d(AB;SD)=AH=a*2căn 6/3