cho tập hợp A= {1, 2, 4, 5, 8, 9 }lấy ngẫu nhiên một số. xác suất để lấy được một số chẵn là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?

Chọn C
Ta có ![]()
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
![]()
![]()
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà ![]()
![]()
![]()
![]() hoặc
hoặc ![]()
Vì ![]()
![]() nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ

![]()
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
![]()
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
![]()
Vậy xác suất cần tìm là 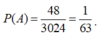

Gọi X là biến cố: “lấy được cả hai viên bi mang số chẵn. “
Gọi A là biến cố: “lấy được viên bi mang số chẵn ở hộp I”. Vì hộp 1 có 4 bi chẵn nên
=> P A = C 4 1 C 9 1 = 4 9 .
Gọi B là biến cố: “lấy được viên bi mang số chẵn ở hộp II”: P B = 3 10 .
Ta thấy biến cố A, B là 2 biến cố độc lập nhau, theo công thức nhân xác suất ta có:
P X = P A . B = P A . P B = 4 9 . 3 10 = 2 15 .
Chọn đáp án A.

Không gian mẫu: n(Ω)= 6
Goị biến cố A:" Lấy được một số chẵn"
A={2;4;8} ➝ n(A)=3
Vậy p(A)=\(\dfrac{n\left(A\right)}{n\left(\Omega\right)}\)=\(\dfrac{3}{6}\)=\(\dfrac{1}{2}\)

Chọn D
*) Ta có: ![]()
*) Tính n(A): Giả sử 8 chữ số được viết vào 8 ô trống được đánh số từ 1 đến 8
TH1: Xếp bất kỳ
Xếp hai chữ số 1, hai chữ số 2 và 4 chữ số còn lại: Có ![]() (cách).
(cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
Xếp hai chữ số 1 đứng liền nhau: Có ![]() cách.
cách.
Xếp hai chữ số 2 đứng liền nhau: Có ![]() cách.
cách.
Số các cách xếp thuộc cả hai trường hợp trên:
+ Coi hai chữ số 1đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
+ Xếp X, Y và 4 số còn lại có: ![]() (cách)
(cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: ![]() (cách)
(cách)
Vậy ![]()
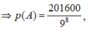

Ko gian mẫu 6 cách
Biến cố A '' lấy được 1 số chẵn '' 3 cách
Xác suất P(A) = 1/2