 Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Vẽ hình và làm giúp em bài này với ạ, Em cảm ơn ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 9:
a: Xét tứ giác OPMN có
góc OPM+góc ONM=180 độ
=>OPMN là tứ giác nội tiếp
b: \(MN=\sqrt{10^2-6^2}=8\left(cm\right)\)
c: ΔOAB cân tại O
mà OH là đường trung tuyến
nên OH vuông góc AB
Xét tứ giác OHNM có
góc OHM=goc ONM=90 độ
=>OHNM là tứ giác nội tiép
=>góc MHN=góc MON

a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp đường tròn đường kính AB
=>I là trung điểm của AB
b: Gọi H là giao của AD và BE
ABDE nội tiếp
=>góc HDE=góc HBA
=>góc HDE=góc HMN
=>DE//MN

a:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc CMO+góc CIO=180 độ
=>CIOM nội tiếp

a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC

1. English is more interesting than music.
2. Today they are not as happy as they were yesterday.
3. Ha Noi is not as small as Hai Duong.
4. Mai's sister is not as pretty as her.
6. You have got more money than me.
7. Art is not as difficult as French.
8. Nam's father is more careful than him.
9. No one in our town is as rich as Mr Ron.
10. He is the most intelligent in my class.
11. Everest is the highest mountain in the world.
12. Minh is the fattest person in my group.
13. I can't swim as far as Jan.
14B 15C 16A 17C 18B 19C 20B

1. What size shoes do you take?
2. What newspaper do you read?
3. What color are your eyes?
4. What time did you arrive this morning?
5. What kind of film do you like?
6. How tall is your teacher?
7. How far is it from your house to the office?
8. How much did you pay for your new shirt?
9. How often do you take an English test in class?
10. How long have you been studying English?

a: Δ=(m-2)^2-4(m-4)
=m^2-4m+4-4m+16
=m^2-8m+20
=m^2-8m+16+4
=(m-2)^2+4>=4>0
=>Phương trình luôn có 2 nghiệm pb
b: x1^2+x2^2
=(x1+x2)^2-2x1x2
=(m-2)^2-2(m-4)
=m^2-4m+4-2m+8
=m^2-6m+12
=(m-3)^2+3>=3
Dấu = xảy ra khi m=3

a.
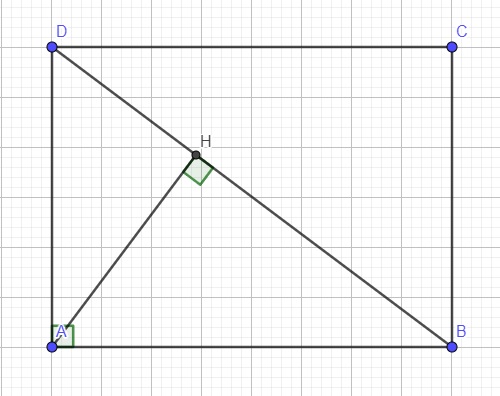
Do ABCD là hình chữ nhật \(\Rightarrow\widehat{HBA}=\widehat{CDB}\) (so le trong)
Xét hai tam giác HBA và CDB có:
\(\left\{{}\begin{matrix}\widehat{HBA}=\widehat{CDB}\left(cmt\right)\\\widehat{AHB}=\widehat{BCD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta CDB\left(g.g\right)\)
b.
Xét hai tam giác AHD và BAD có:
\(\left\{{}\begin{matrix}\widehat{ADB}\text{ chung}\\\widehat{AHD}=\widehat{BAD}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta AHD\sim\Delta BAD\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{DB}=\dfrac{DH}{AD}\Rightarrow AD^2=DH.DB\)
c.
Áp dụng định lý Pitago cho tam giác vuông BAD:
\(DB=\sqrt{AD^2+AB^2}=\sqrt{BC^2+AB^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Theo chứng minh câu b:
\(AD^2=DH.DB\Rightarrow DH=\dfrac{AD^2}{DB}=\dfrac{BC^2}{DB}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
Áp dụng Pitago cho tam giác vuông AHD:
\(AH=\sqrt{AD^2-HD^2}=\sqrt{6^2-3,6^2}=4,8\left(cm\right)\)

Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)









a: góc CAO+góc CMO=180 độ
=>CAOM nội tiếp
b: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) co
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
CD=CM+MD=CA+DB
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
c: AC*BD=CM*MD=OM^2=R^2