Cho tam giác ABC , đường trung tuyến AM. Qua trung điểm O của AM , vẽ đường thẳng cắt các cạnh AB,AC theo thứ tự B',C'.Chứng minh rằng khi đường thẳng thay đổi mà vẫn đi qua O thì tổng AB/AB' + AC/AC' không đổi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 4 2019
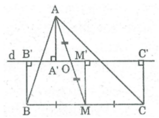
Ta có: BB' ⊥ d (gt)
CC' ⊥ d (gt)
Suy ra: BB'// CC'
Tứ giác BB'C'C là hình thang
Kẻ MM' ⊥ d ⇒ MM' // BB' // CC'
Lại có M là trung điểm của BC nên M' là trung điểm của B’C’
⇒ MM' là đường trung bình của hình thang BB'C'C
⇒ MM' = (BB' + CC') / 2 (1)
* Xét hai tam giác vuông AA'O và MM'O:
∠ (AA'O) = ∠ (MM' O) = 90 0
AO=MO (gt)
∠ (AOA') = ∠ (MOM' ) (2 góc đối đỉnh)
Do đó: ∆ AA'O = ∆ MM'O (cạnh huyền, cạnh góc nhọn)
⇒AA' = MM' (2)
Từ (1) và (2) suy ra: AA' = (BB' + CC') / 2
AH
Akai Haruma
Giáo viên
15 tháng 4 2021
Lời giải:
a) Áp dụng định lý Talet cho:
Tam giác $CFD$ có $AM\parallel FD$:
$\frac{DF}{AM}=\frac{CD}{CM}(1)$
Tam giác $ABM$ có $ED\parallel AM$:
$\frac{ED}{AM}=\frac{BD}{BM}(2)$
Lấy $(1)+(2)\Rightarrow \frac{DE+DF}{AM}=\frac{CD}{BC:2}+\frac{BD}{BC:2}=\frac{BC}{BC:2}=2$
$\Rightarrow DE+DF=2AM$
Vì $AM$ không đổi khi $D$ di động nên $DE+DF$ không đổi khi $D$ di động
b) Dễ thấy $KADM$ là hình bình hành do có các cặp cạnh đối song song. Do đó $KA=DM$
Áp dụng định lý Talet cho trường hợp $AK\parallel BD$:
$\frac{KE}{ED}=\frac{KA}{BD}=\frac{DM}{BD}(3)$
Lấy $(1):(2)$ suy ra $\frac{DF}{ED}=\frac{CD}{BD}$
$\Rightarrow \frac{EF}{ED}=\frac{CD}{BD}-1=\frac{CD-BD}{BD}=\frac{CM+DM-(BM-DM)}{BD}=\frac{2DM}{BD}(4)$
Từ $(3);(4)\Rightarrow \frac{2KE}{ED}=\frac{EF}{ED}$
$\Rightarrow 2KE=EF\Rightarrow FK=EK$ hay $K$ là trung điểm $EF$
19 tháng 11 2017
Ta có: BB’ ⊥ d (gt)
CC’ ⊥ d (gt)
Suy ra: BB’ // CC’
Tứ giác BB’CC’ là hình thang
Kẻ MM’ ⊥ d
⇒ MM’ // BB’ // CC’
Nên MM’ là đường trung bình của hình thang BB’CC’
⇒MM′=BB′+CC′2(1)⇒MM′=BB′+CC′2(1)
Xét hai tam giác vuông AA’O và MM’O:
ˆOA′A=ˆOM′MOA′A^=OM′M^
AO = MO (gt)
ˆAOA′=ˆMOM′AOA′^=MOM′^ (đối đỉnh)
Do đó: ∆ AA’O = ∆ MM’O (cạnh huyền, góc nhọn)
⇒ AA’ = MM’ (2)
Từ (1) và (2) suy ra: AA′=BB′+CC′2AA′=BB′+CC′/2.
4 tháng 1
Giải thích các bước giải:
a.Ta có xy//BC,MD//AB��//��,��//��
→AD//BM,AB//DM→ˆBMA=ˆMAD,ˆBAM=ˆAMD→��//��,��//��→���^=���^,���^=���^
Mà ΔABM,ΔMDAΔ���,Δ��� chung cạnh AM��
→ΔABM=ΔMDA(g.c.g)→Δ���=Δ���(�.�.�)
→AD=BM,MD=AB→��=��,��=��
Tương tự chứng minh được AE=MC,ME=AC��=��,��=��
→DE=DA+AE=BM+MC=BC→��=��+��=��+��=��
→ΔABC=ΔMDE(c.c.c)→Δ���=Δ���(�.�.�)
b.Gọi AM∩BD=I��∩��=�
→ˆIAD=ˆIMB,ˆIDA=ˆIBM(AD//BM)→���^=���^,���^=���^(��//��)
Mà AD=BM��=��
→ΔIAD=ΔIMB(g.c.g)→Δ���=Δ���(�.�.�)
→IA=IM,IB=ID→��=��,��=��
Lại có AE//CM→ˆEAI=ˆIMC��//��→���^=���^
Kết hợp AE=CM��=��
→ΔIAE=ΔIMC(c.g.c)→Δ���=Δ���(�.�.�)
→ˆAIE=ˆMIC→���^=���^
→ˆEIC=ˆAIE+ˆAIC=ˆMIC+ˆAIC=ˆAIM=180o→���^=���^+���^=���^+���^=���^=180�
→E,I,C→�,�,� thẳng hàng
→CE,AM,BD→��,��,�� đồng quy
