Một mặt bàn tròn đồng chất có khối lượng \(m_0=3\left(kg\right)\) đặt trên ba chân thẳng đứng có cùng chiều dài lắp ở sát mép bàn tại các điểm \(A,B,C\) sao cho \(ABC\) là tam giác đều, cạnh \(a=0,6\left(m\right)\). Đặt một vật nhỏ \(m_1\) lên điểm \(M_1\) trên mặt bàn thì áp lực đè lên các chân bàn \(A,B,C\) lần lượt là \(10N,20N,30N.\)
a) Tìm khối lượng \(m_1\) và vị trí \(M_1\) ?
b) Phải đặt vật khối lượng \(m_2\) tối thiểu bằng bao nhiêu, ở vị trí nào trên mặt bàn thì bàn sẽ bị lật ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

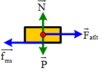
Để vật không bị trượt ra khỏi bàn: F q t l t ≤ F m s
⇒ m ω 2 . r ≤ μ . N = μ . m . g
⇒ ω ≤ μ . g r = 2.10 0 , 8 = 5 r a d / s

Chọn B.
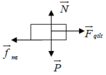
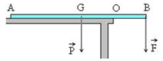
Trục quay tại O.
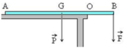
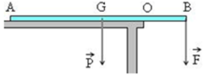
Theo điều kiện cân bằng thì MP/(O) = MF/(O)
→ F.OB = P.OG ↔ F.AB/4=P.AB/4 → P = F = 40 N.

Chọn B.
Trục quay tại O.
Theo điều kiện cân bằng thì M P O = M F O
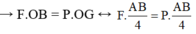
→ P = F = 40 N.

Chọn C
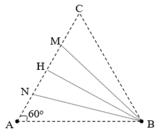
+ Khoảng cách giữa hai cực đại liên tiếp trên AB là 0,5l
+ Vì trên AB có 14 cực đại nên: 7 λ < A B = a ≤ 8 λ
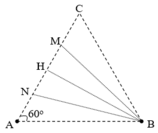
+ Gọi N và M là hai điểm cực đại cùng pha liên tiếp trên AC
Điều kiện cực đại liên tiếp:
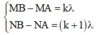
Þ NB – MB + MA – NA = l Û NB – MB + MN = l (1)
Điều kiện cùng pha liên tiếp:
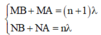
Þ MB – NB + MA – NA = l Û MB – NB + MN = l (2)
Từ (1) và (2) suy ra NB = MB Þ MN = l
+ Gọi H là trung điểm của NM Þ BH ^ AH Þ BH là đường cao trong tam giác đều hạ từ B đến AC. Ta có:
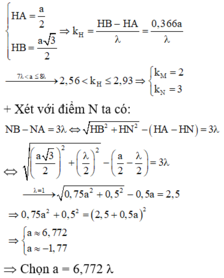

Ta có:
+ f = 1 T = ω 2 π → ω = 2 π f
+ Lực hướng tâm tác dụng vào vật: F h t = m ω 2 r = m 2 π f 2 r
+ Để vật không văng ra khỏi mặt bàn, ta phải có:
F h t = F m s n max ↔ m 2 π f 2 r = F m s n max → f 2 = F m s n max m 4 π 2 r = 0 , 08 20.10 − 3 .4 π 2 .1 = 0 , 101 → f ≈ 0 , 32 s − 1
Vậy muốn vật không bị văng ra khỏi mặt bàn thì tần số quay của bàn lớn nhất là: f = 0 , 32 s − 1
Đáp án: A
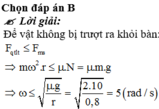
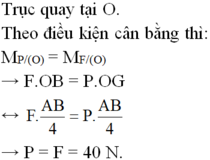

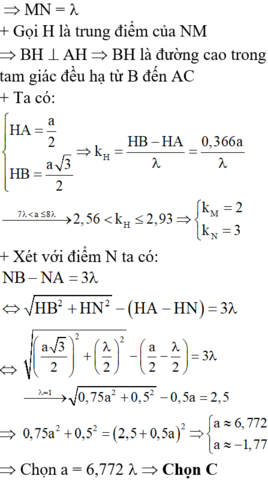
a.
Trọng lượng \(m_1\) bằng tổng trọng lượng của bàn trừ cho trọng lượng mặt bàn: \(P_1=P_A+P_B+P_C-P_{m_o}=10+20+30-30=30N\)
\(\Rightarrow m_{m1}=\dfrac{P}{10}=\dfrac{30}{10}=3kg\)
Vì bàn lúc này đang nằm trong trạng thái cân bằng nên ta áp dụng quy tắc Moment lực: \(P_A\cdot d_A-P_{m_0}\cdot d_{m_0}-P_{m_1}\cdot d_{m_1}=0\)
\(\Leftrightarrow10\cdot\left(0,6+0,6\right)-30\cdot\dfrac{2}{3}\cdot0,6-30\cdot d_{m_1}=0\)
\(\Leftrightarrow0-30d_{m_1}=0\)
\(\Leftrightarrow d_{m_1}=0\left(m\right)\)
Vậy vị trí của \(m_1\) nằm trên BC
b.
Để bàn bị lật thì \(m_2\) phải đối xứng với điểm A sao cho phản lực của A = 0N
Theo quy tắc Moment lực: \(P_{m_0}\cdot d_{m_0}=m_{m_2}\cdot d_{m_2}\cdot g\)
\(\Leftrightarrow12=6m_{m_2}\)
\(\Leftrightarrow m_{m_2}=2\left(kg\right)\)
Câu b mình không chắc lắm nhưng mà không hiểu chỗ nào thì bạn cứ hỏi ha.