Tìm các số nguyên x,y thỏa mãn : xy +12=x+y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
0
TN
0
28 tháng 10 2023
4:
(x+1)(y-2)=5
=>\(\left(x+1;y-2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(0;7\right);\left(4;3\right);\left(-2;-3\right);\left(-6;1\right)\right\}\)
3 tháng 5 2019
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
4 tháng 5 2019
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
LP
0
AH
Akai Haruma
Giáo viên
7 tháng 4 2023
Đoạn (x+1)(y-1)=0 thì dấu phía sau là dấu hoặc (chứ không phải dấu và) bạn ơi.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 4 2023
\(xy\) - \(x\) + \(y\) = 1
(\(xy\) + \(y\)) - \(x\) - 1 = 0
\(y\)(\(x\) + 1) - ( \(x\) + 1) = 0
(\(x\) + 1)( \(y\) - 1) = 0
\(\left[{}\begin{matrix}x+1=0\\y-1=0\end{matrix}\right.\)
⇒\(\left[{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Lời giải:
$xy+12=x+y$
$\Rightarrow xy-x-y=-12$
$\Rightarrow x(y-1)-y=-12$
$\Rightarrow x(y-1)-(y-1)=-11$
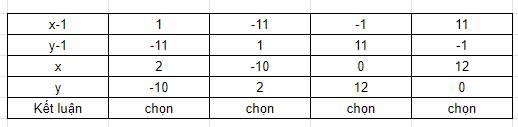
$\Rightarrow (y-1)(x-1)=-11$
Do $x,y$ nguyên nên $x-1,y-1$ cũng nguyên. Ta có bảng:
