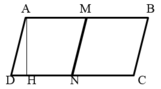
Cho hình bình hành ABCD có M và N là trung điểm của AB và CD. Biết DN=18cm,AH=22cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(có nhiều cách giải)
Hình bên có tất cả 3 hình nình hành gồm AMND, MBCN và ABCD
Vì M và N là trung điểm của AB và CD nên AM = MB = DN = Nc = 18 cm
Diện tích hình bình hành AMND là : 22 x 18 = 369 (cm2)
Tổng diện tích các hình bình hành có trong hình vẽ chính bằng tổng diện tích của 4 hình bình hành AMND là : 396 x 4 = 1584 cm2
Đáp số : 1584 cm2

(có nhiều cách giải)
Hình bên có tất cả 3 hình nình hành gồm AMND, MBCN và ABCD
Vì M và N là trung điểm của AB và CD nên AM = MB = DN = Nc = 18 cm
Diện tích hình bình hành AMND là : 22 x 18 = 369 (cm2)
Tổng diện tích các hình bình hành có trong hình vẽ chính bằng tổng diện tích của 4 hình bình hành AMND là : 396 x 4 = 1584 cm2
Đáp số : 1584 cm2

Nếu không trả lời đầy đủ em bảo chị làm bài giải luôn cho dễ hiểu nhé

a, \(S_{ABCD}\) = AH.CD
= 3.4
= 12 (\(cm^2\))
b, Ta có M là trung điểm AB
⇒ AM = \(\dfrac{AB}{2}\) = \(\dfrac{4}{2}\) = 2 (cm)
\(S_{ADM}\) = \(\dfrac{AH.AM}{2}\)
= \(\dfrac{3.2}{2}\)
= 3 (\(cm^2\))
c, Gọi O là trung điểm
c, Gọi O là trung điểm ND
Từ O kẻ OP // CD
Xét ΔNDC có: NO = OD
OP // CD
⇒ OP là đường trung bình ΔNDC
⇒ OP = \(\dfrac{1}{2}DC\) mà DC = 4 cm
⇒ OP = 2 cm
Xét ΔAMN và ΔPON có:
Góc BAC = góc APO
Góc MOP = góc AMD
AM = ON
⇒ ΔAMN = ΔPON (g.c.g)
⇒ NM = ON mà ON = \(\dfrac{1}{2}DM\)
⇒ DN = 2MN

Sửa đề: DH vuông góc AC
1: Xét ΔHDC có
M,N lần lượt là trung điểm của HD,HC
nên MN là đường trung bình
=>MN//DC và MN=DC/2
=>MN//AB và MN=AB
=>ABNM là hình bình hành
2: NM//AB
=>NM vuông góc AD
Xét ΔAND có
DH,NM là các đường cao
DH cắt NM tại M
=>M là trực tâm
3: Xét ΔHDC có
E,N lần lượt là trung điểm của CD,CH
nên EN là đường trung bình
=>EN//HD và EN=HD/2
=>EN//HM và EN=HM
=>HMEN là hình bình hành
=>MN đi qua trung điểm của HE

AH là gì vậy em .
Với cả đề bài yêu cầu gì vậy em