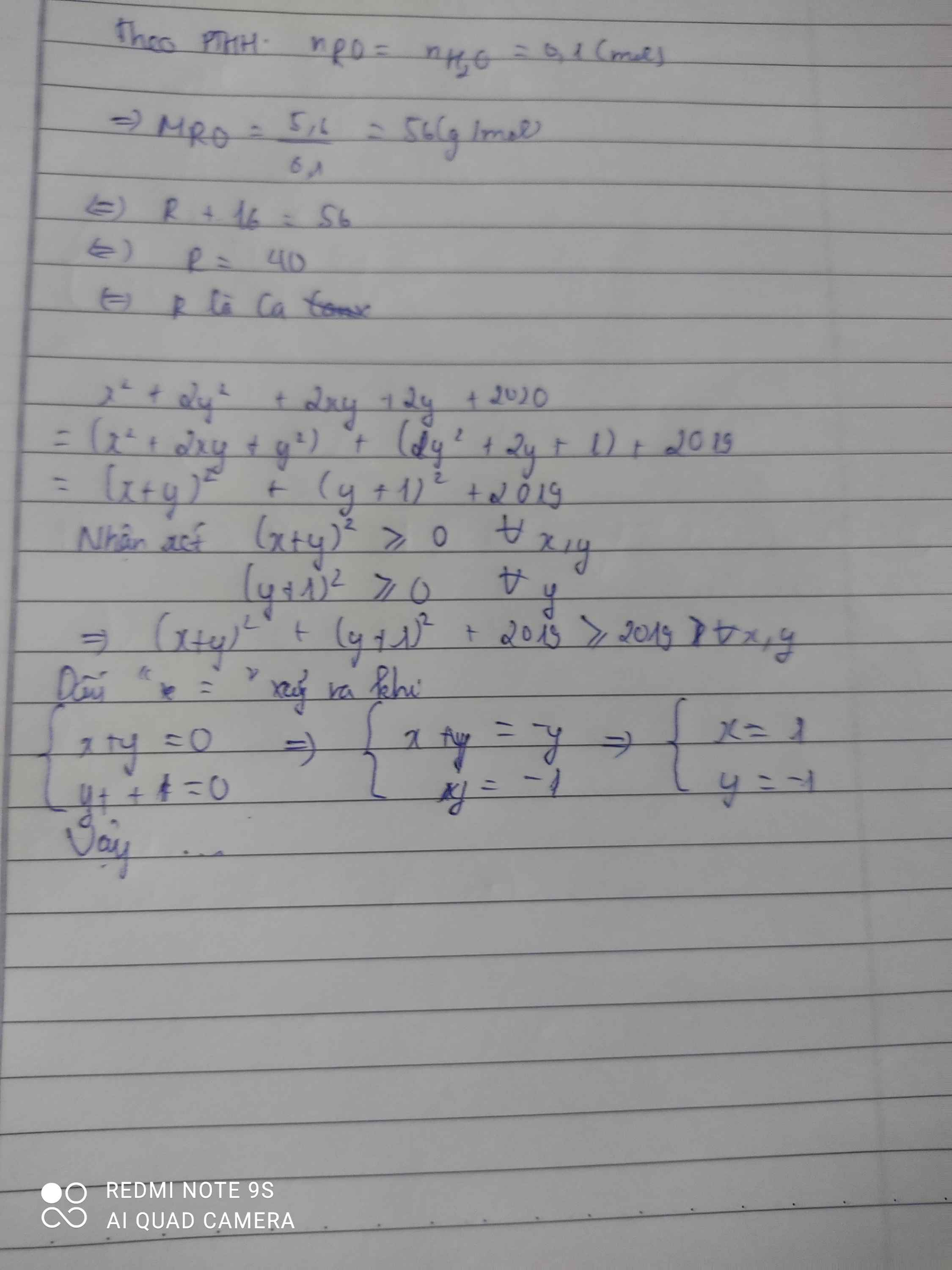cho x^2+y^2=7.Tìm GTLN của:x^2+2y^2+2x-4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
S
1

AH
Akai Haruma
Giáo viên
31 tháng 10 2023
Đề thiếu. Bạn viết lại đề cẩn thận, rõ ràng để mọi người hỗ trợ tốt hơn bạn nhé.
TN
0




MH
9 tháng 2 2022
\(x^2+2y^2+2xy+2y+2020\)
\(=\left(x^2+2xy+y^2\right)+\left(y^2+2y+1\right)+2019\)
\(=\left[\left(x+y\right)^2+\left(y+1\right)^2+2019\right]\ge2019\)
Vì \(\left\{{}\begin{matrix}\left(x+y\right)^2\ge0\forall x,y\\\left(y+1\right)^2\ge0\forall y\end{matrix}\right.\)
Dấu "=" \(\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1\end{matrix}\right.\)
DN
0